От одинаковой задачи – разные пути: как убеждения влияют на освоение физики и программирования

от

Автор: Денис Аветисян

Новое исследование показывает, что личные представления студентов о вычислениях и физике оказывают решающее влияние на их мотивацию и самооценку при использовании компьютерных инструментов в обучении.

Пока крипто-инвесторы ловят иксы и ликвидации, мы тут скучно изучаем отчетность и ждем дивиденды. Если тебе близка эта скука, добро пожаловать.

Купить акции "голубых фишек"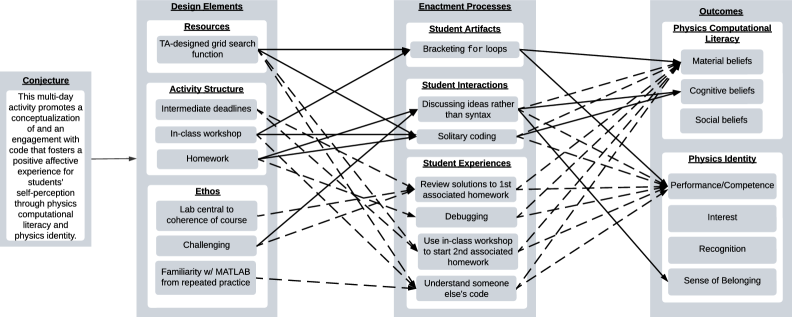
Представленная схема отражает индивидуальное восприятие Бриджит многодневной деятельности, конкретно демонстрируя ее понимание и взаимодействие с кодом, где связи, вызывающие положительные эмоции, обозначены сплошными стрелками, а вызывающие отрицательные - пунктирными.
Представленная схема отражает индивидуальное восприятие Бриджит многодневной деятельности, конкретно демонстрируя ее понимание и взаимодействие с кодом, где связи, вызывающие положительные эмоции, обозначены сплошными стрелками, а вызывающие отрицательные — пунктирными.

В статье представлен анализ сравнительных кейсов с использованием метода конструирования гипотетических карт для выявления взаимосвязи между убеждениями, эмоциональным опытом и формированием идентичности в физике и программировании.

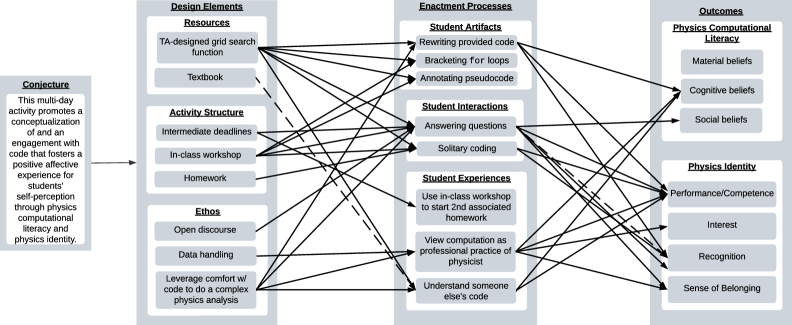
Несмотря на растущее внедрение вычислительных методов в обучение физике, часто упускается из виду влияние этого на формирование идентичности и эмоционального отношения студентов к предмету. В настоящей работе, ‘Same Activity, Divergent Impacts: Representing Paths Towards Physics Computational Literacy and Physics Identity with Conjecture Mapping-Based Narrative Analysis’, представлен сравнительный анализ опыта двух студентов, демонстрирующий, как их предшествующие представления о вычислениях и физике определяют их эмоциональные реакции и самовосприятие при использовании компьютерных инструментов. Анализ, основанный на методе «conjecture mapping», выявляет связь между интерпретацией задания, эпистемическим отношением к коду и манерой взаимодействия с подсказками, формирующими представление о собственной компетентности. Как более глубокое понимание этих индивидуальных траекторий может помочь в разработке эффективных стратегий обучения, способствующих развитию позитивной идентичности будущих физиков?

За пределами вычислений: Необходимость вычислительной грамотности

Традиционные программы обучения физике зачастую делают акцент на символьных преобразованиях и аналитическом решении задач, уделяя недостаточно внимания вычислительным методам. Это приводит к тому, что студенты, несмотря на умение формально оперировать физическими законами, испытывают затруднения при работе с реальными данными и сложными системами. Такой подход препятствует формированию глубокого понимания физических явлений, поскольку ограничивает возможности применения теоретических знаний к практическим задачам и моделированию реальных процессов. Вместо развития интуиции и способности к анализу данных, студенты сосредотачиваются на алгоритмическом применении формул, что негативно сказывается на их способности к самостоятельному научному исследованию и решению нетривиальных проблем, требующих творческого подхода и умения использовать \text{вычислительные инструменты} .

Исследования показывают, что существующий разрыв между теоретическим обучением и возможностью анализа реальных данных существенно ограничивает развитие у студентов так называемой “CognitivePCL” — способности к комплексному познанию и решению проблем в физике. Установлено, что исходные представления о природе знания, или “эпистемические рамки”, оказывают значительное влияние на эмоциональное восприятие студентами собственной компетентности как физиков. Таким образом, недостаточное внимание к практическому применению знаний не только затрудняет понимание сложных систем, но и формирует неуверенность в собственных силах, препятствуя развитию полноценного научного мышления и способности к самостоятельным исследованиям.

Наблюдается существенный разрыв между преподаванием фундаментальных принципов физики и формированием практических навыков, необходимых для современной научной деятельности. Традиционные подходы часто акцентируют внимание на теоретических выкладках и символической манипуляции, в то время как умение работать с реальными данными, моделировать сложные системы и применять вычислительные методы остается недостаточно развитым. Это несоответствие затрудняет переход от абстрактного понимания к решению конкретных задач, ограничивая возможности будущих ученых в исследовании окружающего мира и разработке инновационных технологий. В результате, студенты, обладающие глубокими теоретическими знаниями, могут испытывать трудности при анализе экспериментальных данных или построении физических моделей, что снижает их эффективность в научной среде и замедляет прогресс в различных областях науки и техники.

На основе карты предположений можно увидеть, как Джейк воспринимает многодневную деятельность, отражая его понимание и взаимодействие с кодом через положительные (сплошные стрелки) и отрицательные (пунктирные стрелки) связи.
На основе карты предположений можно увидеть, как Джейк воспринимает многодневную деятельность, отражая его понимание и взаимодействие с кодом через положительные (сплошные стрелки) и отрицательные (пунктирные стрелки) связи.

Иммерсивный опыт: Многодневные проекты как катализаторы

Многодневные исследовательские проекты (“MultiDayActivity”) представляют собой эффективный подход к развитию вычислительной грамотности, поскольку они интегрируют вычислительные методы в контекст реальных научных исследований. Такой формат позволяет студентам применять вычислительные инструменты не как изолированные упражнения, а как неотъемлемую часть процесса научного познания. В рамках этих проектов студенты сталкиваются с задачами, требующими анализа данных, моделирования и интерпретации результатов, что способствует более глубокому пониманию как предметной области, так и вычислительных навыков. Использование вычислительных инструментов в контексте аутентичных научных задач повышает мотивацию и способствует формированию у студентов способности применять эти инструменты для решения реальных проблем.

Многодневные проектные работы предоставляют студентам возможность столкнуться со сложными задачами, требующими применения и совершенствования вычислительных навыков. В процессе работы над проектом студенты последовательно уточняют и улучшают свои алгоритмы и методы анализа данных, переходя от первоначальных, возможно, неоптимальных решений к более эффективным и точным. Этот итеративный процесс включает в себя тестирование, отладку и переработку кода, что способствует глубокому пониманию принципов программирования и вычислительной науки. Особое внимание уделяется не только достижению конечного результата, но и процессу решения задачи, стимулируя критическое мышление и способность к самообучению.

Многодневные практические задания часто включают в себя предоставленный исходный код (ProvidedCode) в качестве отправной точки для анализа данных. В дополнение к этому, используются методы нелинейной аппроксимации (NonLinearFitting) для моделирования сложных зависимостей и алгоритмы поиска по сетке (GridSearch) для оптимизации параметров моделей и выявления наилучших значений, соответствующих экспериментальным данным. Такой подход позволяет студентам сосредоточиться на анализе и интерпретации результатов, а не на разработке базового программного обеспечения, значительно ускоряя процесс обучения и повышая эффективность исследования.

Эффективность многодневных активностей напрямую зависит от их способности предоставлять возможности для активного обучения и решения задач, что влияет на вовлеченность студентов и результаты обучения. Данное понятие, известное как “аффорданс”, относится к тем свойствам активности, которые позволяют студентам эффективно взаимодействовать с материалом и демонстрировать приобретенные навыки. Высокий аффорданс предполагает четкую структуру, доступные ресурсы и возможность для самостоятельного исследования, что способствует более глубокому пониманию и удержанию информации. Активности с низким аффордансом, напротив, могут приводить к фрустрации и снижению мотивации, отрицательно сказываясь на итоговых результатах. Оценка и оптимизация аффорданса многодневных активностей является ключевым фактором для повышения их образовательной ценности.

Поддержка на пути к успеху: Развитие навыков решения вычислительных задач

Стратегическая поддержка, или “scaffolding”, играет ключевую роль в успешном освоении студентами навыков решения вычислительных задач. Данный подход подразумевает предоставление временной, структурированной помощи, адаптированной к текущему уровню знаний и навыков учащегося. В контексте вычислительной физики, это может включать в себя предоставление готовых фрагментов кода, упрощенных моделей, пошаговых инструкций или примеров решения аналогичных задач. Целью является не просто предоставление ответа, а содействие развитию самостоятельности и способности к решению проблем, путем постепенного снижения уровня поддержки по мере роста компетенций студента. Эффективное “scaffolding” обеспечивает возможность преодоления сложных задач, которые могли бы быть недоступны без внешней помощи, и способствует формированию уверенности в собственных силах.

Поддержка студентов в процессе решения вычислительных задач не только развивает их когнитивные навыки в области Computational Problem-Solving Learning (CognitivePCL), но и оказывает прямое влияние на формирование их профессиональной идентичности в физике (PhysicsIdentity). Успешное преодоление сложностей благодаря ассистенции способствует повышению уверенности в своих способностях и компетенциях, что критически важно для долгосрочного вовлечения в научную деятельность и осознания себя как компетентного физика-исследователя. Повышение уровня компетенции и уверенности напрямую коррелирует с укреплением PhysicsIdentity и формированием позитивного отношения к изучению физики с использованием вычислительных методов.

Эффективное построение образовательных траекторий, или «scaffolding», предполагает поэтапное уменьшение объема предоставляемой помощи по мере освоения учащимися необходимых навыков. Этот подход не ограничивается простой демонстрацией решения, а включает в себя структурированную поддержку, направленную на развитие самостоятельности и уверенности в своих силах. На начальных этапах может использоваться подробное пошаговое руководство или предоставление готовых фрагментов кода, однако с прогрессом в обучении акцент смещается на стимулирование самостоятельного поиска решений и критического анализа, что способствует формированию внутренней мотивации и самоэффективности. Постепенное снижение уровня поддержки позволяет студентам не только освоить конкретные вычислительные методы, но и развить способность к самостоятельному решению новых задач.

Поддержка когнитивного развития студентов посредством поэтапного обучения, известного как “scaffolding”, является ключевым фактором в формировании уверенных и компетентных специалистов в области вычислительной физики. Этот подход позволяет учащимся постепенно осваивать сложные концепции и методы, развивая навыки решения задач и критического мышления. Успешное применение “scaffolding” способствует не только углублению понимания физических принципов, но и формированию позитивного отношения к вычислительному моделированию как эффективному инструменту научного исследования. В результате, студенты приобретают не только технические навыки, но и уверенность в своих способностях, что необходимо для успешной карьеры в области вычислительной физики.

Формирование идентичности: Развитие чувства принадлежности

Формирование устойчивой «физической идентичности» — это не просто субъективное восприятие себя как человека, интересующегося физикой, но и ключевой фактор, определяющий настойчивость и успех студентов в естественно-научных и технических областях. Исследования показывают, что студенты, уверенные в своей способности понимать и применять физические принципы, с большей вероятностью преодолевают трудности, сохраняют мотивацию и добиваются значительных результатов в учебе и будущей профессиональной деятельности. Эта идентичность формируется в процессе освоения предмета, взаимодействия с преподавателями и сверстниками, а также в зависимости от личного опыта и предшествующих представлений о науке. Укрепление этой идентичности требует создания поддерживающей образовательной среды, где студенты чувствуют себя частью научного сообщества и получают признание своих усилий и достижений.

Исследования показывают, что положительный опыт, получаемый студентами при работе с вычислительной физикой, играет значительную роль в формировании чувства принадлежности к научному сообществу. Особенно важна поддержка в виде структурированного подхода — так называемого “scaffolding”, когда сложные задачи разбиваются на более мелкие, управляемые этапы. Иммерсивные активности, предполагающие глубокое погружение в предметную область, позволяют студентам не только усвоить теоретический материал, но и почувствовать себя активными участниками научного процесса. Такой подход способствует развитию уверенности в собственных силах и формированию позитивной идентичности как физиков, что, в свою очередь, оказывает влияние на их мотивацию и дальнейшие успехи в области STEM.

Исследования показывают, что открытое обсуждение и признание вклада студентов являются ключевыми факторами, укрепляющими их уверенность и мотивацию в изучении физики. Когда студентам предоставляется возможность свободно выражать свои мысли, задавать вопросы и делиться своими решениями, это способствует формированию чувства сопричастности и принадлежности к научному сообществу. Признание их усилий, будь то положительная обратная связь, публичное признание достижений или включение их идей в дальнейшую работу, значительно повышает их самооценку и стимулирует к дальнейшему обучению. Данный подход позволяет студентам не просто усваивать материал, но и чувствовать себя ценными участниками научного процесса, что, в свою очередь, положительно влияет на их успеваемость и стремление к карьере в области физики.

Исследование подчеркивает, что формирование позитивной «Физической Идентичности» у студентов напрямую зависит от устранения неравенства в доступе к образовательным возможностям. Предыдущие представления о природе знания, сформированные до начала обучения, оказывают значительное влияние на то, как студенты воспринимают себя в роли физиков. Особенно важным фактором является вовлечение в практическую деятельность с использованием вычислительных методов, позволяющее преодолеть барьеры, связанные с недостаточным опытом или предвзятыми представлениями. Успешное развитие этой идентичности требует целенаправленных усилий по обеспечению равных возможностей для всех студентов, независимо от их происхождения или предыдущей подготовки, что способствует увеличению представленности различных групп в области физики и стимулирует инновации.

Исследование, представленное в статье, демонстрирует, что восприятие вычислительных инструментов и их интеграция в физическое образование тесно связаны с уже существующими убеждениями студентов. Это подтверждает необходимость критического подхода к преподаванию, где не просто передаются знания, а формируется способность к сомнению и проверке. Как однажды заметил Лев Давидович Ландау: «В науке нет места вере, только — проверке». Именно такая установка, нацеленная на последовательную проверку гипотез и признание возможности ошибки, позволяет студентам формировать не только вычислительную грамотность, но и глубокое понимание физических принципов, а также развивать свою научную идентичность, как показано в анализе траекторий студентов посредством conjecture mapping.

Куда же дальше?

Представленные данные, как и любые другие, не открывают истину, а лишь освещают её фрагменты. Настоящая ценность исследования заключается не в констатации связи между изначальными представлениями студента и его опытом освоения вычислительных методов в физике, а в осознании масштаба этой неопределенности. Кажется, что проблема не в самих вычислительных инструментах, а в устоявшихся рамках, в которых студенты воспринимают физику и вычисления — и, что более важно, в неспособности адекватно оценить границы этих рамок.

Дальнейшие исследования должны сместить фокус с поиска «лучших» методов обучения на разработку инструментов для выявления и корректировки ошибочных предпосылок. Попытки создать универсальную «подготовку» к вычислительной физике обречены на провал, если не учитывать разнообразие когнитивных и аффективных факторов, формирующих индивидуальное восприятие. Необходим переход от анализа «данных» к анализу ошибок в данных, к выявлению систематических искажений, возникающих на стыке дисциплинарных представлений.

Истинная мудрость, вероятно, заключается в признании того, что любая модель, даже самая элегантная, является лишь упрощением реальности. Будущие работы должны сосредоточиться на разработке методов, позволяющих студентам осознавать размер своей погрешности, а не стремиться к иллюзии абсолютного знания. Возможно, тогда вычислительная физика перестанет быть просто инструментом, а станет способом критического мышления.

Оригинал статьи: https://arxiv.org/pdf/2601.10005.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-01-17 22:50