Эмоции и физика: как дизайн обучения влияет на восприятие

Автор: Денис Аветисян

Новое исследование показывает, как согласованность между намерениями преподавателя и пониманием студентом важности задания формирует его эмоциональный опыт в процессе обучения физике с использованием вычислительных инструментов.

Пока крипто-инвесторы ловят иксы и ликвидации, мы тут скучно изучаем отчетность и ждем дивиденды. Если тебе близка эта скука, добро пожаловать.

Купить акции "голубых фишек"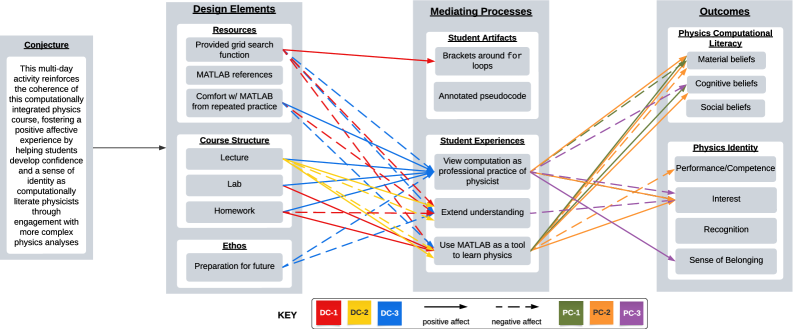

На основе анализа многодневной деятельности, карта предположений отражает восприятие Бриджет о влиянии согласованности между общей программой и рассматриваемым действием, демонстрируя, как целостность курса способствует пониманию конкретных задач.

Анализ влияния дизайна обучения на аффективный опыт студентов в интегрированном курсе физики с использованием метода построения предположений.

Несмотря на признанную важность вычислительных методов в обучении физике, их влияние на эмоциональную сферу студентов остаётся малоизученным. В работе «Studying Impact and Intent of Design: Conjecture Mapping for Affect-Centered Analysis» представлено исследование, в котором с помощью модифицированной карты предположений проанализирована связь между намерениями преподавателя и восприятием студентом деятельности в рамках интегрированного курса современной физики. Полученные результаты демонстрируют, что согласованность между педагогическими целями и субъективной оценкой значимости задания формирует эмоциональный опыт студента, влияя на его уверенность в своих вычислительных навыках и идентификацию с физикой. Какие ещё методики могут помочь выявить и скорректировать расхождения между задуманным и реальным эффектом образовательных инициатив?

Преодолевая Разрыв: Интеграция Вычислений в Физику

Традиционное преподавание физики зачастую рассматривает вычислительные методы как дополнительный, необязательный элемент, а не как неотъемлемую часть фундаментальных концепций. Этот подход приводит к тому, что студенты испытывают трудности при применении вычислительного мышления к решению сложных физических задач и оказываются недостаточно подготовленными к современной исследовательской работе. Вместо того, чтобы органично вплетать вычислительные задания в процесс изучения основных принципов, курсы физики нередко предлагают их в виде отдельных, изолированных упражнений или факультативных проектов. Это создает разрыв между теоретическими знаниями и практическими навыками, необходимыми для успешного применения физических законов в реальных ситуациях и для проведения численного моделирования сложных систем, таких как $N$ -частичные системы или динамика жидкостей.

Отсутствие тесной связи между теоретическим обучением физике и вычислительными методами существенно ограничивает возможности студентов в решении сложных задач, требующих применения алгоритмического мышления. Традиционный подход, фокусирующийся на аналитических решениях, зачастую не позволяет развить навыки, необходимые для моделирования реальных физических систем и анализа больших объемов данных, что особенно критично в современных исследованиях. Студенты, не владеющие навыками программирования и численного моделирования, испытывают трудности при переходе к практической работе, будь то научные исследования или инженерные разработки, поскольку все чаще требуется не просто понимание физических принципов, но и умение применять их в вычислительных экспериментах и симуляциях. В результате, подготовка будущих физиков и инженеров может оказаться недостаточной для решения задач, стоящих перед современной наукой и технологиями.

Необходим принципиальный сдвиг в подходах к физическому образованию, заключающийся в органичном вплетении вычислительных задач в саму структуру обучения. Вместо рассмотрения вычислений как дополнительного инструмента, они должны стать неотъемлемой частью процесса освоения физических принципов. Такой подход позволяет студентам не просто решать задачи, но и глубже понимать лежащие в их основе концепции, развивая интуицию и способность к моделированию сложных систем. Когда вычислительные методы тесно связаны с теоретическим материалом, они становятся мощным средством для визуализации абстрактных идей, проверки гипотез и исследования физических явлений, недоступных для аналитического решения. Это, в свою очередь, значительно повышает эффективность обучения и готовит будущих специалистов к решению реальных научных и инженерных задач, требующих комплексного подхода и умения работать с большими объемами данных.

Эффективная интеграция вычислительных методов в физическое образование требует тщательного сопоставления этих методов с общими целями и содержанием курса. Недостаточно просто добавить программирование как отдельный модуль; вычислительные задачи должны быть органично вплетены в изучение физических концепций, служа не только инструментом решения задач, но и средством углубления понимания лежащих в их основе принципов. Например, моделирование физических явлений, таких как $F = ma$ , или анализ данных, полученных в ходе виртуальных экспериментов, позволяют студентам увидеть, как абстрактные математические формулы воплощаются в реальных процессах. При этом, выбор вычислительных инструментов и задач должен соответствовать уровню подготовки студентов и специфике изучаемого материала, обеспечивая не усложнение, а упрощение и углубление усвоения ключевых понятий.

Построение Вычислительных Лесов: Поддержка Обучения

Постепенное введение вычислительных задач, известное как вычислительное опорунивание (computational scaffolding), является критически важным для поддержки обучения физике. Этот подход предполагает последовательное наращивание сложности задач, начиная с простых и понятных, и постепенно переходя к более сложным, требующим интеграции нескольких навыков. Опорунивание обеспечивает временную поддержку, позволяя студентам справляться с задачами, которые они не смогли бы выполнить самостоятельно, и способствует развитию самостоятельности в решении физических задач с использованием вычислительных методов. Эффективное опорунивание позволяет студентам не только освоить конкретные вычислительные навыки, но и глубже понять физические принципы, лежащие в основе решаемых задач.

Эффективное проектирование учебных заданий является основным механизмом реализации вычислительной поддержки обучения, позволяя последовательно интегрировать вычислительные задачи в процесс изучения физики. Это достигается посредством разработки заданий, которые постепенно увеличивают сложность и требуют от студентов применения все более сложных вычислительных инструментов и навыков. Ключевым аспектом является структурирование заданий таким образом, чтобы они обеспечивали постепенное освоение необходимых вычислительных компетенций, необходимых для решения физических задач, а также способствовали развитию навыков программирования и анализа данных. Тщательно спланированная последовательность заданий должна обеспечивать поддержку на каждом этапе, позволяя студентам применять полученные знания и навыки в новых контекстах и углублять понимание как физических принципов, так и вычислительных методов.

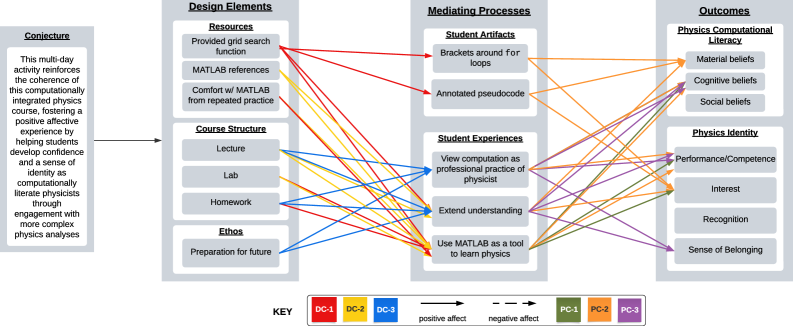
Картирование предположений (conjecture mapping) представляет собой аналитический метод, используемый для оценки соответствия между задуманными целями при разработке учебных заданий и фактическими результатами обучения студентов. Этот подход предполагает детальное сопоставление предполагаемых студентами гипотез, лежащих в основе решения задач, с ожидаемыми ответами и демонстрируемым пониманием физических принципов и вычислительных навыков. Анализ расхождений между предполагаемыми и фактическими результатами позволяет выявить проблемные области в дизайне заданий и внести коррективы для повышения эффективности обучения, обеспечивая более тесную связь между теоретическими знаниями и практическими навыками студентов.

Последовательно выстроенная серия учебных заданий, направленных на постепенное усложнение вычислительных задач, способствует формированию более глубокого понимания как физических принципов, так и навыков программирования. Такой подход позволяет студентам осваивать сложные концепции, начиная с базовых операций и постепенно переходя к более сложным алгоритмам и моделям. Инструментальное использование вычислений в контексте физических задач не только укрепляет понимание физики, но и развивает вычислительное мышление, необходимое для решения широкого круга научных и инженерных задач. Важно, чтобы каждое задание опиралось на ранее полученные знания и навыки, создавая прочную основу для дальнейшего обучения.

Данная схема отображает видение профессора Эванса относительно взаимосвязи между общей структурой курса и рассматриваемым многодневным мероприятием, демонстрируя предполагаемую когерентность между ними.

Статистическая Основа: Фундамент Вычислительной Физики

Прочная статистическая база является основой для эффективного применения вычислительных методов в физике. Физические задачи часто требуют анализа больших объемов данных и оценки неопределенностей, что невозможно без глубокого понимания статистических концепций, таких как распределения вероятностей ( $P(x)$ ), математическое ожидание, дисперсия и статистические тесты. Вычислительные методы, такие как метод Монте-Карло, напрямую зависят от генерации случайных чисел и статистического анализа полученных результатов для получения надежных оценок физических величин. Понимание статистических погрешностей и методов их уменьшения, включая выбор оптимальных алгоритмов и размеров выборок, критически важно для получения осмысленных результатов моделирования и анализа данных.

Развитие когнитивной вычислительной физической грамотности (CognitivePCL) является следствием прочной статистической базы и позволяет студентам применять новые подходы к решению сложных задач. CognitivePCL подразумевает не просто владение инструментами моделирования, но и способность к критическому анализу результатов, пониманию ограничений используемых методов и формулированию физически обоснованных моделей. Это включает в себя умение абстрагироваться от конкретных деталей реализации и фокусироваться на физической сути явления, а также способность к адаптации знаний и навыков для решения новых, нестандартных проблем. Формирование CognitivePCL позволяет студентам перейти от простого применения готовых алгоритмов к самостоятельному проектированию и интерпретации численных экспериментов.

Практическое владение вычислительными инструментами и синтаксисом (MaterialPCL) не является самоцелью, а формируется и укрепляется на основе развитого когнитивного понимания принципов вычислительной физики. Эффективное использование программных пакетов, языков программирования и численных методов требует от студента не просто знания команд, но и способности логически структурировать задачу, выбирать подходящие алгоритмы и интерпретировать полученные результаты. Поэтому, развитие MaterialPCL напрямую зависит от предварительного формирования CognitivePCL — способности критически мыслить и решать сложные задачи с использованием вычислительных методов. Без достаточного когнитивного понимания, освоение синтаксиса и инструментов остается поверхностным и ограничивает возможности применения вычислений в физических исследованиях.

Владение несколькими языками программирования, или «вычислительная многоязычность», значительно расширяет возможности студента в области вычислительной физики. Это позволяет не ограничиваться синтаксическими и функциональными особенностями одного конкретного языка, а адаптировать алгоритмы и подходы к различным вычислительным средам и задачам. Способность переносить навыки и знания между языками, такими как Python, C++, Fortran или MATLAB, повышает гибкость и эффективность при решении сложных физических проблем, а также облегчает интеграцию различных инструментов и библиотек в единый вычислительный процесс. $\text{Например, использование Python для прототипирования и анализа данных, а затем перенос критически важных участков кода на C++ для оптимизации производительности.}$ В конечном итоге, вычислительная многоязычность способствует развитию более глубокого понимания принципов программирования и вычислительной физики в целом.

Формирование Физической Идентичности через Вычислительное Вовлечение

Исследования показывают, что целенаправленная связь вычислительных задач с реальными физическими приложениями и профессиональной практикой значительно повышает профессиональную релевантность обучения. Когда студенты видят, как осваиваемые ими навыки напрямую применимы в решении практических задач, встречающихся в работе физиков, это способствует более глубокому пониманию материала и формированию чувства причастности к научному сообществу. Такая связь позволяет не просто изучать абстрактные концепции, но и увидеть их воплощение в конкретных технологиях и исследованиях, что, в свою очередь, мотивирует к дальнейшему развитию в выбранной области и укрепляет уверенность в собственных силах как будущего специалиста.

Формирование устойчивой физической идентичности — это процесс, в ходе которого студент начинает воспринимать себя как часть научного сообщества физиков. Эта идентичность не сводится лишь к знанию формул и решению задач, но и включает в себя ощущение принадлежности, уверенность в собственных силах и способность мыслить как физик. Когда учебные задания напрямую связаны с реальными физическими явлениями и профессиональной деятельностью, студенты лучше осознают применимость полученных знаний, что способствует укреплению их самовосприятия как компетентных исследователей. Такая связь между теорией и практикой позволяет студентам не просто заучивать материал, но и интегрировать его в свою картину мира, тем самым способствуя формированию прочной и осознанной физической идентичности.

Эмоциональная вовлеченность, включающая в себя как переживаемые эмоции, так и внутреннюю мотивацию, играет ключевую роль в формировании физической идентичности студента. Исследования показывают, что простого усвоения знаний недостаточно для ощущения себя частью научного сообщества. Когда учебный процесс вызывает искренний интерес и положительные эмоции, у студентов развивается более глубокое понимание предмета и растет уверенность в собственных силах. Эта внутренняя убежденность, подкрепленная позитивным опытом, способствует формированию устойчивого самовосприятия как физика, что, в свою очередь, влияет на дальнейший выбор образовательной траектории и профессиональной деятельности. Таким образом, создание учебной среды, учитывающей эмоциональные потребности студентов, является важным фактором успешного формирования их профессиональной идентичности.

Исследования показали, что между заявленными целями обучения и фактическим эмоциональным опытом студентов может возникать несоответствие. Данный разрыв подчеркивает критическую важность согласованности между структурой курса и предлагаемыми видами деятельности. Когда учебный процесс не вызывает положительных эмоций или не соответствует ожиданиям учащихся, это негативно сказывается на формировании их профессиональной идентичности и мотивации. Поэтому, для эффективного обучения физике, необходимо тщательно продумывать не только содержание, но и способы его подачи, обеспечивая соответствие между теоретическими задачами и практическими упражнениями, а также учитывая эмоциональное вовлечение студентов.

Исследование демонстрирует, что понимание взаимосвязи между намерениями преподавателя и восприятием студента имеет решающее значение для формирования позитивного аффективного опыта в обучении физике. Анализ посредством конъюнктурного картирования позволяет выявить расхождения между ожидаемыми результатами и реальным восприятием, что критически важно для адаптации образовательных стратегий. Как однажды заметил Нильс Бор: «Противоположности не отменяют друг друга, они дополняют». Данная фраза отражает суть исследования: кажущиеся противоречия между целями обучения и личным опытом студента, при правильном анализе, могут привести к более глубокому пониманию и, как следствие, к эффективному обучению. Понимание этой закономерности — ключ к оптимизации образовательного процесса.

Что дальше?

Представленная работа, исследуя соотнесение намерений преподавания и восприятия студентами значимости учебной деятельности, неизбежно сталкивается с проблемой субъективности. Изучение аффективной сферы, как показывает опыт, всегда сопряжено с риском редукции сложного опыта к упрощенным категориям. Каждое отклонение от ожидаемой модели — не ошибка, а потенциальный сигнал о скрытых зависимостях, требующих более глубокого анализа. В дальнейшем необходимо сместить акцент с констатации когерентности между намерением и восприятием на выявление механизмов, посредством которых расхождения формируют и переформируют познавательную идентичность.

Особый интерес представляет исследование роли “шума” — случайных факторов, не связанных напрямую с учебным контентом или педагогическим подходом. Игнорирование этих факторов — распространенная ошибка, однако именно они могут раскрыть неожиданные аспекты аффективного обучения. Более того, необходимо разработать методы, позволяющие отслеживать динамику аффективного состояния студента в реальном времени, не ограничиваясь ретроспективными оценками. Это потребует интеграции различных инструментов, включая физиологические датчики и методы анализа текста.

В конечном счете, задача состоит не в создании идеальной системы преподавания, а в понимании того, как студенты конструируют собственное знание, опираясь на свои аффективные переживания. Изучение этих процессов — бесконечный поиск, требующий не только строгости научного анализа, но и готовности к принятию неопределенности и противоречий. Понимание системы — это исследование её закономерностей, а не поиск однозначных ответов.

Оригинал статьи: https://arxiv.org/pdf/2601.09878.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-01-18 00:31