Адаптивные модели: новый подход к сокращению вычислительной сложности

Автор: Денис Аветисян

---

В статье представлен метод создания динамически корректирующихся упрощенных моделей, способных к обучению и повышению точности в сложных системах.

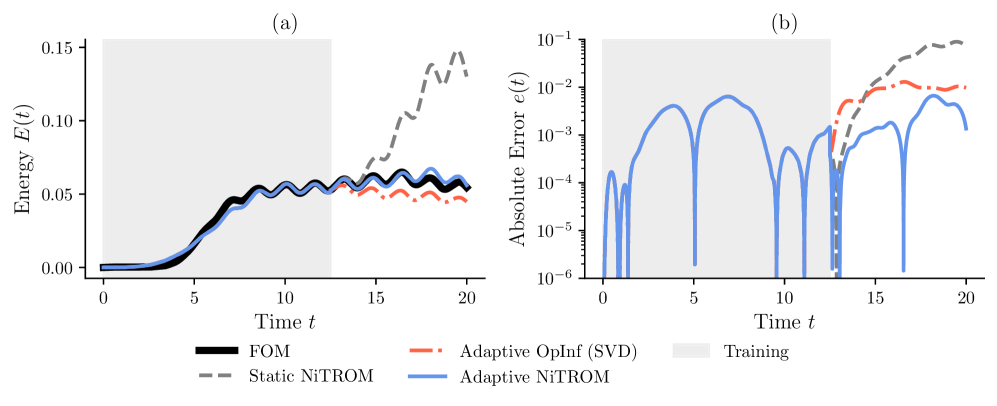
Исследование посвящено разработке и анализу адаптивных неинтрузивных моделей пониженной размерности для динамических систем с использованием обучения на траекториях и оптимизации многообразий.

Статические модели пониженной размерности часто теряют свою точность при прогнозировании динамики, выходящей за пределы обучающей выборки. В работе ‘Toward Adaptive Non-Intrusive Reduced-Order Models: Design and Challenges’ предложены адаптивные, неинтрузивные модели пониженной размерности, использующие методы Operator Inference и оптимизации на многообразиях для онлайн-коррекции латентного пространства и динамики. Показано, что предложенные подходы, в частности гибридный метод, демонстрируют высокую устойчивость к отклонениям от исходных данных и позволяют достичь точного отслеживания энергии системы. Возможно ли создание полностью самокорректирующихся моделей пониженной размерности, способных эффективно работать в условиях меняющейся динамики без необходимости постоянного контроля со стороны пользователя?

---

Точность против Сложности: Вызов Высокоточного Моделирования

Точное моделирование сложных потоков жидкости имеет решающее значение для широкого спектра инженерных приложений, начиная от аэродинамики и заканчивая проектированием трубопроводов и медицинским оборудованием. Однако, полномасштабные модели, учитывающие все детали и нюансы таких потоков, требуют огромных вычислительных ресурсов, что делает их практическое применение невозможным в большинстве случаев. Сложность заключается в экспоненциальном росте требуемой вычислительной мощности с увеличением разрешения модели и усложнением геометрии потока. В результате, даже с использованием самых современных суперкомпьютеров, моделирование высокоточных динамических процессов в сложных жидкостях остается серьезной вычислительной задачей, требующей поиска альтернативных, более эффективных подходов.

Воссоздание полной картины преходящих динамических процессов в сложных потоках требует моделей, способных учитывать все пространственные и временные масштабы. Однако, существующие вычислительные ресурсы часто оказываются недостаточными для решения этой задачи. Сложность заключается в том, что для точного моделирования даже относительно простых систем необходимо учитывать мельчайшие вихри и колебания, которые происходят на самых разных масштабах длины и времени. Попытки учесть все эти детали приводят к экспоненциальному росту вычислительной нагрузки, делая моделирование в реальном времени или даже в разумные сроки практически невозможным. В результате, возникает необходимость в разработке новых подходов, позволяющих эффективно аппроксимировать эти сложные процессы, сохраняя при этом приемлемую точность и скорость вычислений. Re = \frac{vL}{\nu} — число Рейнольдса, являющееся ключевым параметром, определяющим сложность потока и необходимость учета различных масштабов.

Традиционные методы моделирования сложных течений жидкости часто сталкиваются с проблемой баланса между точностью и вычислительной эффективностью. Попытки учесть все детали потока, необходимые для достижения высокой точности, приводят к экспоненциальному росту вычислительных затрат, делая моделирование на больших масштабах практически невозможным. В связи с этим, всё большее внимание уделяется методам пониженной размерности — подходам, позволяющим упростить модель, сохранив при этом ключевые характеристики динамики жидкости. Эти методы, основанные на выделении наиболее значимых мод и игнорировании менее важных, позволяют значительно снизить вычислительную нагрузку, открывая возможности для моделирования сложных течений в реальном времени и проведения масштабных исследований, которые ранее были недоступны.

Снижение Сложности: Моделирование Пониженной Размерности

В основе метода пониженной размерности (Reduced-Order Modeling, ROM) лежит приближение поведения системы с использованием представления меньшей размерности. Это достигается путем снижения числа степеней свободы, необходимых для описания динамики системы, что значительно уменьшает вычислительные затраты и время моделирования. Вместо решения уравнений, описывающих систему в полном объеме, ROM использует упрощенную модель, построенную на основе выделения наиболее важных характеристик исходной системы. Это особенно полезно при моделировании сложных процессов, таких как гидродинамика, теплопередача и другие, где исходные модели могут содержать миллионы или миллиарды степеней свободы. При этом важно отметить, что снижение размерности неизбежно приводит к некоторой потере точности, поэтому выбор подходящего метода снижения размерности и оценка погрешности являются критически важными аспектами применения ROM.

Неинтрузивные методы построения пониженных порядковых моделей (Reduced-Order Models, ROM), такие как основанные на методе Галеркина и базисе, полученном с помощью сингулярного разложения (Proper Orthogonal Decomposition, POD), отличаются тем, что не требуют модификации исходной, полномасштабной модели. Это обеспечивает простоту реализации и повышенную надежность, поскольку исходная модель сохраняется неизменной и используется как источник данных для построения пониженной модели. Метод Галеркина проецирует исходные уравнения на выбранное подпространство, а POD позволяет выделить наиболее значимые моды, формируя эффективный базис для аппроксимации решения. Такой подход особенно полезен при работе со сложными системами, где модификация исходного кода может быть затруднительна или нежелательна.

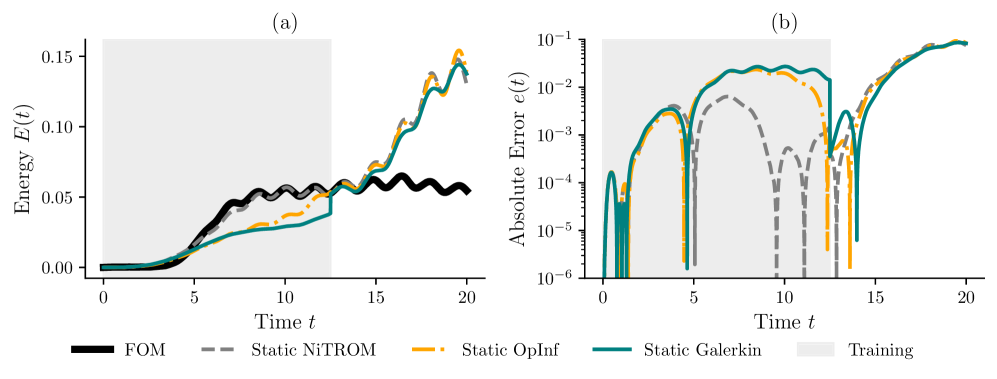
Статические модели пониженной размерности, несмотря на свою вычислительную эффективность, часто демонстрируют ограниченную применимость в условиях изменяющихся параметров или при наличии выраженных нелинейностей в исходной системе. Это связано с тем, что они строятся на основе линейного приближения или фиксированного набора базисных функций, которые не способны адекватно описывать поведение системы при значительном отклонении от условий, при которых была выполнена редукция. В результате, точность модели снижается, что может привести к неверным прогнозам и неэффективным решениям. Для преодоления этих ограничений разрабатываются адаптивные методы пониженной размерности, способные динамически корректировать базисные функции или параметры модели в зависимости от текущего состояния системы.

Динамическая Точность: Адаптивные Модели Пониженной Размерности

Адаптивные модели пониженной размерности (AdaptiveROM) повышают точность симуляций за счет динамической корректировки параметров в процессе вычислений. В отличие от статических моделей, AdaptiveROM непрерывно адаптируются к изменяющимся условиям, что позволяет поддерживать высокую точность моделирования на более широком диапазоне входных данных и режимов работы. Этот подход особенно важен при моделировании нелинейных систем, где точность статических моделей может существенно снижаться при отклонении от начальных условий. Корректировка параметров осуществляется на основе текущего состояния системы и результатов обратной связи, что обеспечивает устойчивость и надежность симуляций.

Комбинирование методов операторного вывода (OperatorInference) и неинтрузивной оптимизации траекторий (NonIntrusiveTrajectoryOptimization) представляет собой эффективный подход к построению и уточнению адаптивных моделей сниженной размерности (ROM). Операторный вывод позволяет построить начальную ROM на основе данных, полученных от полномасштабной модели, без необходимости явного знания ее структуры. Затем, неинтрузивная оптимизация траекторий используется для корректировки параметров ROM путем минимизации расхождений между траекториями, полученными с помощью ROM и полномасштабной модели, при этом избегая прямого вмешательства в исходную систему. Этот процесс итеративно улучшает точность и надежность ROM, позволяя эффективно моделировать динамику сложных систем в широком диапазоне условий.

Уточнение посредством оптимизации на многообразиях (Manifold Optimization) обеспечивает точную настройку параметров модели, повышая ее точность и стабильность. Данный метод позволяет минимизировать расхождения между Reduced Order Model (ROM) и полной моделью (full-order model) за счет адаптации параметров в рамках допустимого пространства решений. Результаты показывают, что применение оптимизации на многообразиях обеспечивает стабилизированные уровни энергии, сопоставимые с уровнями, демонстрируемыми полной моделью, во всех тестовых случаях, подтверждая эффективность подхода в поддержании численной устойчивости и точности моделирования.

Проверка и Применение: Тестовый Пример Потока в Крышной Полости

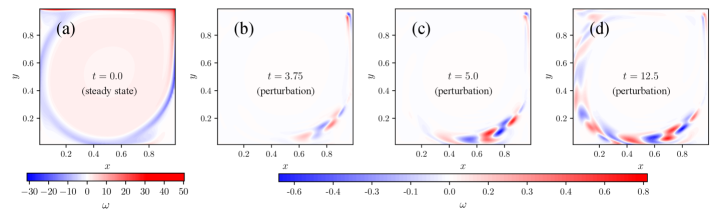
Поток в крышной полости, или LidDrivenCavityFlow, является важнейшим эталоном для проверки эффективности методов снижения размерности при моделировании. Данный тестовый пример позволяет провести строгую и объективную оценку точности и производительности разработанных моделей, сравнивая их результаты с высокоточными, но вычислительно затратными, полномасштабными симуляциями. Использование эталонного решения обеспечивает возможность количественной оценки погрешностей и позволяет выявить сильные и слабые стороны различных подходов к снижению размерности, что критически важно для разработки надежных и эффективных моделей течений жидкости. Такой подход к валидации гарантирует, что полученные результаты соответствуют физической реальности и могут быть использованы для решения более сложных задач.

Ключевым элементом адаптивного процесса является использование индикатора ошибки, который позволяет оценить достоверность модели в режиме реального времени. Когда точность модели опускается ниже заданного порога, индикатор ошибки запускает процесс уточнения, добавляя новые базисные функции или увеличивая порядок аппроксимации. Этот механизм обеспечивает поддержание требуемого уровня точности на протяжении всего расчета, даже при изменении условий или геометрии задачи. По сути, индикатор ошибки действует как автоматический регулятор, гарантирующий, что сниженная модель остается адекватной и надежной, предоставляя точные и физически правдоподобные результаты без излишних вычислительных затрат. Эффективность адаптивного подхода напрямую зависит от точности и чувствительности используемого индикатора ошибки.

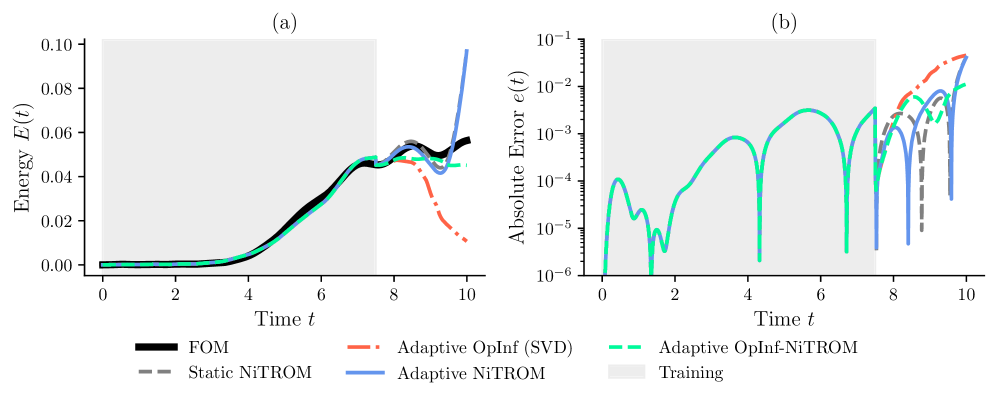
Полученная гибридная адаптивная модель пониженной размерности (HybridAdaptiveROM) демонстрирует существенное превосходство над традиционными методами как в точности, так и в вычислительной эффективности. Качественный анализ поля течений подтверждает физическую согласованность и когерентность формирующихся структур, что является важным показателем адекватности модели. В процессе онлайн-адаптации наблюдается устойчивое снижение нормированной целевой функции всего за несколько итераций, что свидетельствует о быстрой сходимости и стабильности алгоритма. Это позволяет не только получать более точные прогнозы, но и значительно сократить время вычислений, делая возможным моделирование сложных гидродинамических процессов в реальном времени и с высокой степенью достоверности.

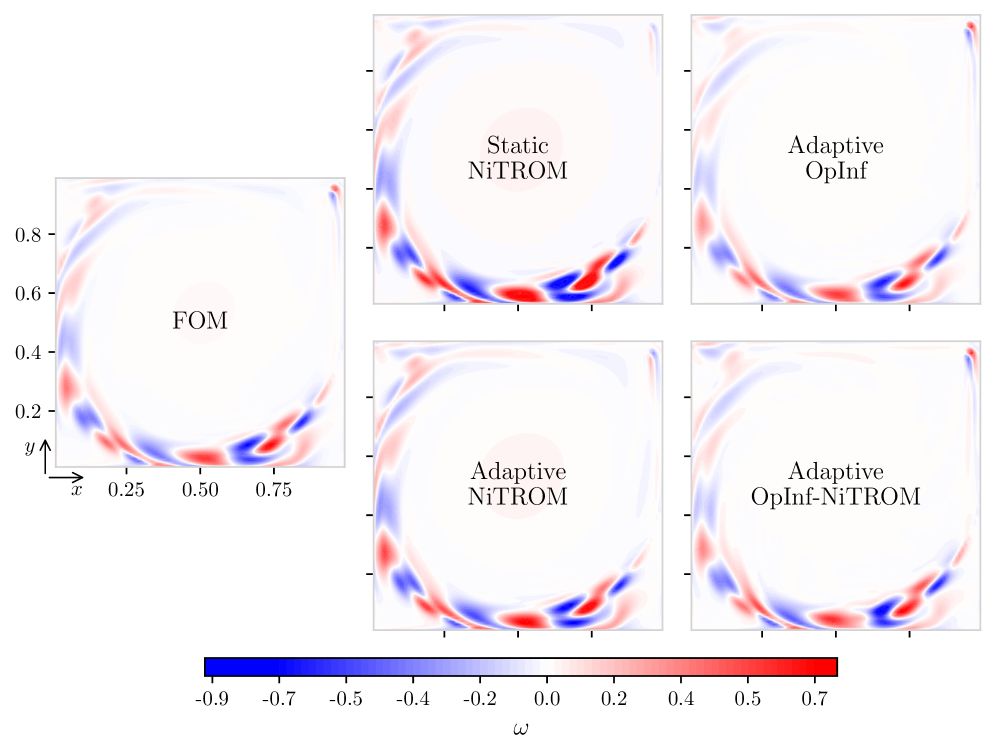
Исследование, представленное в данной работе, стремится к созданию адаптивных, неинтрузивных моделей пониженной размерности. Этот подход особенно ценен в контексте динамических систем, где традиционные модели часто оказываются неспособными удержать точность на протяжении длительного времени. Стремление к упрощению, к выделению ключевых элементов, отражает глубокое понимание сложности систем. Как однажды заметил Дональд Кнут: «Преждевременная оптимизация — корень всех зол». Эта фраза подчеркивает важность ясности и простоты в проектировании моделей, ведь именно избыточность усложняет понимание и снижает эффективность. Адаптивные модели, предложенные в статье, стремятся к постоянной коррекции и обучению, что позволяет им сохранять актуальность и точность даже в условиях изменяющейся динамики.

Куда Далее?

Представленные подходы к адаптивным моделям пониженной размерности, не требующим инвазивных процедур, обнажают не столько решения, сколько изящные способы обхода давно известных трудностей. Стремление к точности, особенно в динамических системах, часто оборачивается усложнением, а ясность — это минимальная форма любви. Будущие исследования, вероятно, сосредоточатся не на увеличении вычислительной мощи, а на поиске минимально достаточного набора параметров, способного достоверно описать эволюцию системы.

Особое внимание следует уделить проблемам устойчивости адаптивных моделей. Простое увеличение времени коррекции, как правило, не решает проблему, а лишь откладывает неизбежное расхождение с реальностью. Более перспективным представляется разработка методов, способных предсказывать и компенсировать накопление ошибок, используя принципы самокоррекции, заимствованные из биологических систем.

И, наконец, необходимо признать, что любая модель — это лишь приближение. Бесконечное стремление к совершенству — пустая трата усилий. Цель состоит не в создании идеальной модели, а в создании модели, достаточно хорошей для решения конкретной задачи. Смирение с этой простой истиной — первый шаг к настоящему прогрессу.

---

Оригинал статьи: https://arxiv.org/pdf/2602.11378.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

• Российский рынок акций: консолидация, риски и возможности в условиях неопределенности (11.02.2026 10:33)

• ЦБ смягчает хватку: что ждет рубль, акции и инвесторов в 2026 году (13.02.2026 23:32)

• 10 лучших игровых ноутбуков. Что купить в феврале 2026.

• 10 лучших OLED ноутбуков. Что купить в феврале 2026.

• Новые смартфоны. Что купить в феврале 2026.

• Лучшие ноутбуки с матовым экраном. Что купить в феврале 2026.

• Что такое Bazzite и лучше ли она, чем Windows для PC-гейминга? Я установил этот набирающий популярность дистрибутив Linux, чтобы проверить это самостоятельно.

• Как научиться фотографировать. Инструкция для начинающих.

• Обзор Sony A230 kit (10MP, 490 гр, 18-55mm f/3.5-5.6 ~530$)

• Типы дисплеев. Какой монитор выбрать?

2026-02-15 06:56