Геометрический интеллект: как нейросети решают головоломки Танграма

Автор: Денис Аветисян

Новое исследование показывает, что современные модели, объединяющие зрение и язык, способны значительно улучшить свои навыки в решении задач, требующих понимания геометрии и пространственного мышления.

Пока крипто-инвесторы ловят иксы и ликвидации, мы тут скучно изучаем отчетность и ждем дивиденды. Если тебе близка эта скука, добро пожаловать.

Купить акции "голубых фишек"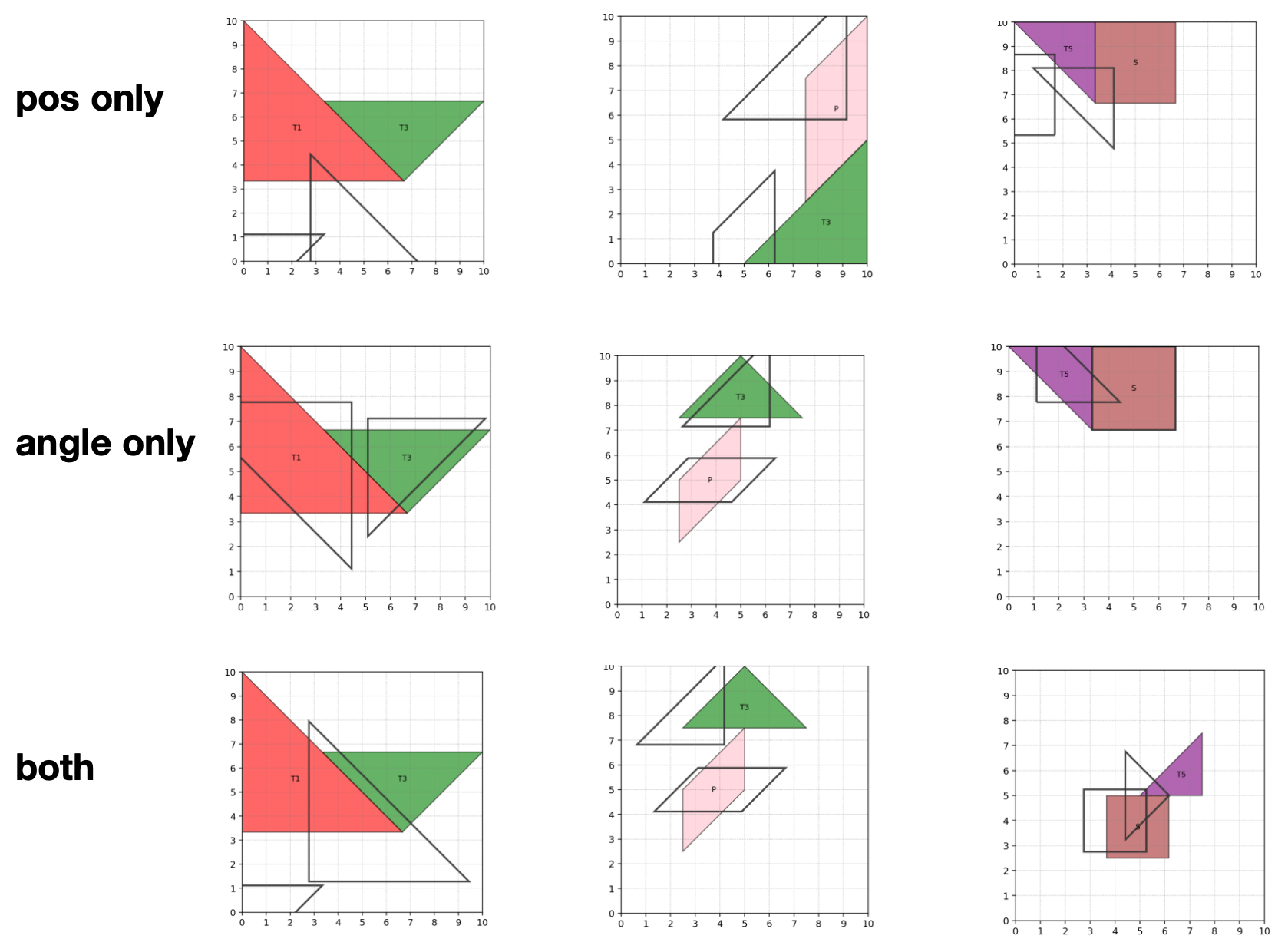

Исследование демонстрирует способность к пространственному мышлению посредством задач, требующих сборки фигур из одной или двух частей танграма.

Исследователи продемонстрировали, что модели способны к самосовершенствованию во время решения головоломок Танграма, используя итеративную доработку и обратную связь без дополнительного обучения.

Несмотря на успехи в области компьютерного зрения и обработки естественного языка, модели, способные к надежному пространственному мышлению, остаются сложной задачей. В данной работе, ‘TangramSR: Can Vision-Language Models Reason in Continuous Geometric Space?’, исследуется способность современных Vision-Language Models (VLMs) решать задачи, требующие непрерывного геометрического рассуждения, используя в качестве примера сборку головоломки Танграм. Предложенная схема самосовершенствования в процессе тестирования, основанная на итеративной доработке предсказаний и обратной связи, позволила значительно повысить точность решения задач — с 0.63 до 0.932 — без переобучения модели. Способны ли мы, вдохновляясь когнитивными механизмами человека, создать самообучающиеся системы, способные к надежному пространственному рассуждению в непрерывных пространственных областях?

Пространственное мышление: Основа интеллекта и ментальной манипуляции

Человеческий интеллект в своей основе неразрывно связан со способностью к пространственному мышлению — умением воспринимать и взаимодействовать с окружающим миром посредством анализа и обработки пространственных отношений. Эта когнитивная функция позволяет не просто ориентироваться в физическом пространстве, но и мысленно манипулировать объектами, прогнозировать их перемещения и решать сложные задачи, требующие визуализации и понимания геометрии. Способность к пространственному анализу проявляется в самых различных аспектах повседневной жизни, от чтения карт и сборки мебели до оценки расстояний и предсказания траекторий движения, и является ключевым компонентом когнитивных способностей человека, определяющим его адаптивность и успешность в решении проблем.

В основе способности человека к решению пространственных задач лежит процесс ментальной ротации — когнитивный механизм, позволяющий мысленно поворачивать и представлять объекты в различных ориентациях. Исследования показывают, что эффективность ментальной ротации тесно связана со способностью к визуально-пространственному мышлению и играет ключевую роль в широком спектре когнитивных функций. От распознавания образов и сборки конструкторов до навигации в пространстве и даже понимания сложных чертежей — ментальная ротация является незаменимым инструментом, позволяющим человеку эффективно взаимодействовать с окружающим миром и решать возникающие проблемы, требующие мысленного манипулирования объектами.

Способность к ментальной ротации и манипулированию объектами в уме является краеугольным камнем более широкого спектра когнитивных процессов, известных как пространственное мышление. Оно играет решающую роль не только в простых задачах, таких как ориентация в пространстве и поиск пути, но и в сложных видах деятельности, требующих решения проблем и планирования. Например, сборка мебели по инструкции, визуализация траектории полета, или даже оценка вероятности успеха определенной стратегии в шахматах — все это требует активного использования пространственного мышления. Более того, исследования показывают, что развитие этих когнитивных способностей напрямую связано с успехом в математике, науке и инженерном деле, подчеркивая их фундаментальную важность для интеллектуальной деятельности человека.

Понимание основных когнитивных механизмов, лежащих в основе пространственного мышления, является первостепенным шагом на пути к созданию действительно интеллектуальных систем. Исследования в области когнитивной психологии и нейробиологии позволяют выявить принципы, по которым мозг обрабатывает пространственную информацию, осуществляя вращение объектов в уме, планирование маршрутов и решение задач, требующих визуализации. Воссоздание этих процессов в искусственном интеллекте — сложная задача, но её решение открывает перспективы для создания машин, способных к гибкому мышлению, адаптации к изменяющимся условиям и эффективному взаимодействию с окружающим миром. Именно поэтому детальный анализ когнитивных способностей человека становится ключевым элементом в разработке алгоритмов и архитектур, лежащих в основе продвинутых интеллектуальных систем.

Итеративное уточнение: Переход от статических предсказаний к динамическому пониманию

Современные системы искусственного интеллекта (ИИ) часто основываются на однократных, статических предсказаниях, выполненных в начале выполнения задачи. Это означает, что после первоначального прогноза система не обладает встроенными механизмами для последовательного улучшения понимания ситуации или корректировки своих выводов в процессе взаимодействия с окружающей средой. В результате, если первоначальное предсказание оказалось неточным или неполным, система не способна адаптироваться и продолжает действовать на основе устаревшей информации, что ограничивает её эффективность и надежность в динамичных условиях. Отсутствие итеративного улучшения понимания является существенным ограничением для решения сложных задач, требующих постоянной адаптации к меняющимся обстоятельствам.

Итеративное уточнение представляет собой альтернативный подход к работе искусственного интеллекта, основанный на цикле: предсказание, оценка и коррекция. В отличие от систем, использующих статические прогнозы, данный метод предполагает последовательное улучшение понимания задачи по мере ее выполнения. На каждом этапе система генерирует прогноз, сравнивает его с фактическим результатом, выявляет расхождения и вносит корректировки в модель для повышения точности последующих предсказаний. Этот процесс позволяет AI адаптироваться к изменяющимся условиям и повышать надежность в сложных задачах, требующих высокой степени точности и адаптивности.

Процесс итеративной доработки в системах искусственного интеллекта существенно зависит от визуальной обратной связи. Визуальная информация, получаемая из окружающей среды, служит ключевым фактором для оценки точности текущих предсказаний и последующей корректировки действий. Анализ визуальных данных позволяет системе определять расхождения между предсказанным состоянием и реальным, что, в свою очередь, инициирует цикл переоценки и внесения изменений в модель. Эффективность визуальной обратной связи напрямую влияет на способность ИИ адаптироваться к динамически меняющимся условиям и обеспечивать точное выполнение пространственных задач, особенно в сложных и непредсказуемых средах.

Постоянная корректировка предсказаний позволяет системам искусственного интеллекта достигать повышенной точности и надежности при решении сложных пространственных задач. В отличие от статических предсказаний, итеративный процесс, включающий сравнение предсказаний с реальными данными и внесение соответствующих изменений, позволяет алгоритмам адаптироваться к изменяющимся условиям и неточностям. Этот подход особенно важен в задачах, требующих навигации, манипулирования объектами или распознавания сцен, где небольшие ошибки в предсказаниях могут привести к значительным отклонениям от желаемого результата. Повышение робастности достигается за счет снижения чувствительности к шумам и неполноте информации, что критически важно для работы в реальных условиях.

Процесс создания набора данных включает в себя преобразование исходных SVG-силуэтов в JSON-аннотации (тип, положение, угол, размер), последующую отрисовку в обучающие/оценочные изображения и разделение на подмножества, состоящие из отдельных элементов, пар элементов или полного танграма.

Геометрическое рассуждение и эталоны для оценки

Геометрическая согласованность является ключевым фактором во многих задачах, требующих пространственного мышления. Она отражает степень соответствия предсказываемых форм базовым геометрическим принципам и правилам. Отклонения от этих принципов, такие как нарушение углов, пропорций или взаимного расположения элементов, снижают качество решения задачи. Оценка геометрической согласованности часто проводится количественно, например, через метрику IoU (Intersection over Union), позволяющую измерить степень перекрытия предсказанной формы с эталонной. Высокий уровень геометрической согласованности указывает на способность модели к точному представлению и манипулированию пространственными данными.

Головоломка «Танграм» представляет собой эффективный инструмент для оценки возможностей моделей в области геометрического мышления, поскольку требует одновременного распознавания фигур и их точного выравнивания. Для решения задач, основанных на «Танграме», модели должны идентифицировать отдельные геометрические примитивы, а затем правильно сопоставить и разместить их относительно друг друга для формирования целевой фигуры. Это предъявляет высокие требования к способности модели к пространственному анализу и точному построению геометрических зависимостей, что делает «Танграм» полезным бенчмарком для проверки и сравнения различных подходов к геометрическому рассуждению.

Начальные результаты тестирования пяти визуально-языковых моделей (VLM) на задаче распознавания отдельных элементов головоломки «Танграм» показали среднее значение метрики IoU (Intersection over Union) на уровне 0.41. Данный показатель указывает на значительные трудности, с которыми сталкиваются модели даже при решении простейших задач по сопоставлению и выравниванию базовых геометрических фигур. Низкое значение IoU свидетельствует о неточностях в определении границ фигур и их корректном позиционировании, что подчеркивает необходимость дальнейшего совершенствования алгоритмов геометрического выравнивания.

При оценке пяти визуально-языковых моделей (VLM) средний показатель Intersection over Union (IoU) при решении задач на составление фигур из двух элементов составил 0.23. Этот результат демонстрирует значительные трудности, с которыми сталкиваются модели при интеграции нескольких геометрических элементов в единую композицию. Низкий IoU указывает на неточное выравнивание и позиционирование отдельных частей, что подчеркивает сложность задачи для современных VLM и необходимость дальнейших исследований в области геометрического рассуждения.

Успешное решение задач, подобных головоломке «Танграм», требует навыка непрерывного геометрического рассуждения, который подразумевает последовательное применение геометрических принципов для анализа и трансформации форм. Этот навык выходит за рамки простого распознавания объектов и включает в себя оценку относительного положения, размера и ориентации фигур, а также предвидение последствий их изменения. Важность непрерывного геометрического рассуждения проявляется в широком спектре реальных приложений, включая робототехнику, компьютерное зрение, проектирование и навигацию, где требуется точное пространственное понимание и планирование действий в динамической среде.

Самосовершенствование посредством вознаграждения и оценки положения

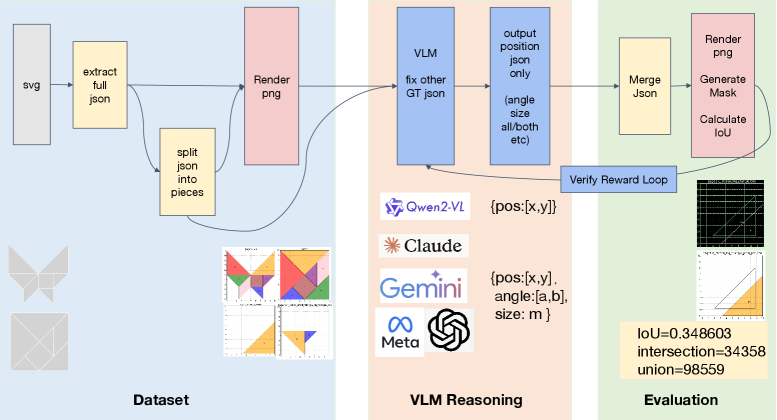
В рамках работы продемонстрировано, что модели способны к улучшению собственной производительности непосредственно в процессе инференса, без какой-либо дополнительной тренировки или обновления параметров. Такое самосовершенствование достигается за счет применения алгоритмов, позволяющих корректировать прогнозы на основе внутренних оценок и обратной связи, формируемой в ходе работы. Этот подход позволяет модели итеративно приближаться к оптимальному решению, адаптируясь к конкретным входным данным и повышая точность предсказаний без необходимости в ресурсоемком переобучении. Фактически, модель способна «обучаться на ходу», используя лишь информацию, доступную в момент предсказания, что открывает перспективы для применения в динамичных и меняющихся средах.

Процесс самосовершенствования модели достигается посредством циклов обратной связи, управляемых вознаграждением. В основе этого подхода лежит принцип положительного подкрепления: модель последовательно уточняет свои прогнозы, получая “награду” за каждое приближение к правильному ответу. Этот механизм стимулирует итеративное улучшение, позволяя системе самостоятельно корректировать свои действия без необходимости переобучения параметров. Фактически, модель учится на своих ошибках в процессе работы, постепенно оптимизируя свои предсказания и повышая точность.

Точность определения положения играет ключевую роль в процессе самосовершенствования модели в ходе работы. В рамках системы, основанной на вознаграждениях, необходимо, чтобы предсказания модели максимально точно соответствовали реальному положению объекта. Именно это соответствие позволяет правильно оценить «награду» за предсказание, и, следовательно, эффективно направить процесс итеративной коррекции. Неточное определение положения приводит к ошибочной оценке и, как следствие, к неправильной корректировке предсказаний, препятствуя достижению оптимальных результатов. Таким образом, высокоточная оценка положения является фундаментом для успешной реализации самообучения модели без обновления параметров, позволяя ей постепенно улучшать свою производительность в процессе выполнения задачи.

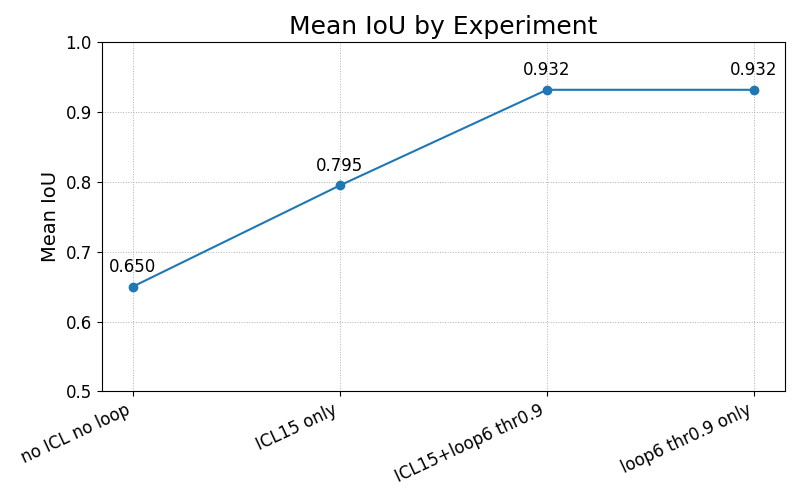
Предложенная архитектура продемонстрировала значительное улучшение точности, выраженное в росте показателя IoU (Intersection over Union) с 0.63 до 0.932 при решении задач, связанных с распознаванием средних по сложности треугольников. Примечательно, что данное повышение производительности было достигнуто без какого-либо обучения модели, что свидетельствует о потенциале самосовершенствования системы в процессе работы. Такой результат подчеркивает возможность создания интеллектуальных систем, способных к адаптации и повышению эффективности без необходимости в традиционных методах обучения с использованием размеченных данных, открывая новые перспективы в области компьютерного зрения и робототехники.

Для количественной оценки погрешности и последующей самокоррекции модель использует вычисление $L2$ -расстояния между предсказанной и фактической позициями. Этот подход позволяет определить степень отклонения предсказания от реальности, предоставляя численную меру ошибки. Чем меньше $L2$ -расстояние, тем точнее предсказание. Используя это значение как сигнал обратной связи, модель способна итеративно улучшать свои прогнозы, корректируя свои действия для минимизации расхождения с целевой позицией, даже без обновления параметров обучения. Такая возможность самокоррекции в процессе работы открывает новые перспективы для повышения надежности и точности моделей в различных приложениях.

Использование цикла самосовершенствования во время тестирования (ICL + вознаграждение) обеспечивает наибольший прирост средней IoU на треугольнике среднего размера.

Исследование демонстрирует, что современные модели, работающие с изображениями и текстом, способны к значительному улучшению навыков пространственного мышления, решая геометрические задачи, такие как головоломка танграм. Этот процесс самосовершенствования во время тестирования, основанный на итеративном уточнении и обратной связи, подчеркивает важность понимания системы как единого целого. Как однажды заметил Джон фон Нейманн: «В науке нет места для тех, кто не умеет думать абстрактно». Этот принцип находит отражение в способности моделей к адаптации и решению сложных задач без переобучения, демонстрируя элегантность дизайна, рожденного из простоты и ясности структуры.

Что дальше?

Представленная работа демонстрирует любопытную способность языковых моделей к визуальному мышлению, проявляющуюся в решении геометрических задач. Однако, кажущееся совершенствование в процессе самообучения во время тестирования — это лишь поверхностное проявление более глубокого принципа. Важно понимать, что данная архитектура, подобно любому сложному механизму, имеет свои пределы. Улучшение производительности без переобучения, безусловно, элегантно, но не отменяет необходимости исследования фундаментальных ограничений подобных систем в понимании непрерывного геометрического пространства.

Очевидным направлением дальнейших исследований представляется расширение класса задач, требующих не только пространственного, но и логического мышления. Способность модели к решению головоломок типа Tangram — это, скорее, демонстрация умения находить паттерны, нежели истинное понимание геометрических принципов. Необходимо оценить, насколько данная архитектура масштабируется на более сложные сценарии, требующие абстрактного мышления и планирования.

Наконец, важно помнить о хрупкости любой системы, основанной на итеративном улучшении. Небольшое изменение входных данных или параметров обучения может привести к неожиданным и непредсказуемым результатам. Исследование устойчивости и надежности подобных моделей — задача, требующая пристального внимания, чтобы избежать создания иллюзии интеллекта, скрывающей за собой потенциальные ошибки.

Оригинал статьи: https://arxiv.org/pdf/2602.05570.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-02-07 23:47