Искривление пространства: как геометрия управляет волнами в мозге

Автор: Денис Аветисян

Новое исследование показывает, что кривизна поверхности влияет на распространение спиральных волн, выступая в роли физической силы, способной стабилизировать паттерны активности и направлять их распространение.

Пока крипто-инвесторы ловят иксы и ликвидации, мы тут скучно изучаем отчетность и ждем дивиденды. Если тебе близка эта скука, добро пожаловать.

Купить акции "голубых фишек"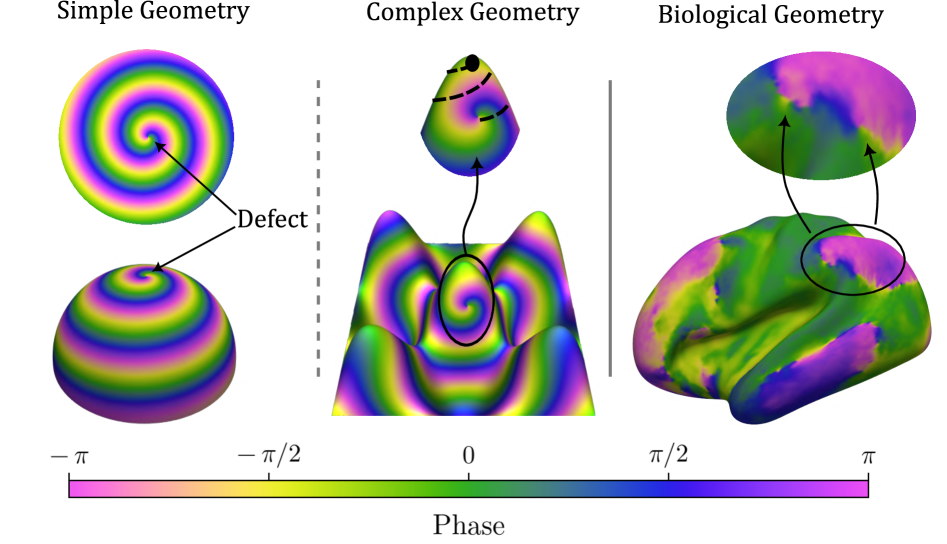

Кривизна поверхности определяет динамику дефектов спиральных волн: моделирование на простых поверхностях демонстрирует устойчивые конфигурации дефектов, в то время как на поверхностях со сложной кривизной наблюдается неустойчивая динамика, что подтверждается экспериментальными данными, полученными на коре головного мозга, где дефекты демонстрируют подвижные траектории, охватывающие значительные области коры.

Исследование демонстрирует, что искривление поверхности оказывает влияние на спиральные волны через эффективную диффузию, выступая в роли геометрической силы, способной модулировать их динамику и пространственное распределение.

Несмотря на повсеместность спиральных волн в неравновесных системах, влияние геометрии поверхности, на которой они распространяются, долгое время оставалось за пределами внимания. В работе «Неравновесные геометрические силы управляют спиральными волнами на сложенных поверхностях» показано, что кривизна поверхности фундаментально формирует поведение спиральных волн, выступая в роли активного физического фактора. Установлено, что градиенты эффективной диффузии, возникающие из-за кривизны, создают геометрические силы, воздействующие на дефекты спиральных волн, стабилизируя и локализуя их на поверхности коры головного мозга. Может ли этот универсальный геометрический механизм объяснить организацию динамических процессов не только в нейронных сетях, но и в других осциллирующих, химических и активных средах?

Спиральные Волны: Универсальный Принцип Самоорганизации

Спиральные волны — это самоорганизующиеся структуры, обнаруживаемые в самых разнообразных системах, от химических реакций, таких как реакция Белоусова-Жаботинского, до сложных биологических процессов. В химических системах эти волны возникают как результат неравномерного распределения химических веществ и их взаимодействия, создавая видимые спиральные узоры, распространяющиеся во времени и пространстве. Аналогичные паттерны наблюдаются в различных биологических контекстах, включая распространение возбуждения в нервных сетях, движение клеток и даже формирование определенных биологических структур. Удивительно, что, несмотря на различия в физической природе этих систем, принцип самоорганизации, лежащий в основе формирования спиральных волн, остается общим, что указывает на универсальность этого явления и его фундаментальную роль в природе.

Спиральные волны, наблюдаемые в различных системах — от химических реакций до биологических процессов — не являются просто визуальными эффектами. Они представляют собой фундаментальные механизмы передачи информации и координации действий. Эти самоорганизующиеся паттерны позволяют системам эффективно обмениваться сигналами и синхронизировать свою деятельность, даже при отсутствии централизованного управления. Например, в химических средах спиральные волны могут кодировать информацию о концентрации веществ, а в биологических тканях — координировать клеточные процессы. Способность этих волн поддерживать и распространять информацию делает их ключевыми элементами в сложных системах, обеспечивая надежную и эффективную коммуникацию между их компонентами.

Изучение динамики спиральных волн открывает перспективы для понимания принципов, применимых в различных областях науки. Установлено, что закономерности, наблюдаемые при формировании и распространении этих волн, обнаруживают поразительное сходство с процессами, происходящими в коре головного мозга. Это позволяет предположить, что спиральные волны могут играть ключевую роль в нейронных вычислениях, обеспечивая эффективный механизм для обработки и передачи информации. Кроме того, принципы самоорганизации, лежащие в основе формирования спиральных волн, представляют интерес для разработки новых вычислительных систем, способных к адаптации и обучению, вдохновленных природными процессами. Понимание этих фундаментальных механизмов может привести к созданию инновационных технологий в области искусственного интеллекта и нейроморфных вычислений.

Исследования коры головного мозга выявили наличие волновых паттернов, удивительно напоминающих спиральные волны, наблюдаемые в различных химических и биологических системах. Эти волны не являются просто побочным продуктом нейронной активности; они предположительно играют ключевую роль в процессах обработки информации. Ученые полагают, что спиральные волны могут служить механизмом для координации активности различных областей коры, обеспечивая эффективную передачу сигналов и, возможно, лежа в основе сложных когнитивных функций. Предположение о волновом характере нейронных вычислений открывает новые перспективы в понимании работы мозга и может привести к разработке принципиально новых подходов к созданию искусственного интеллекта, имитирующего эффективность и гибкость биологических нейронных сетей.

Геометрия Формирует Динамику: Влияние Кривизны на Волны

Искривление поверхности вносит геометрический потенциал, который изменяет поведение спиральных волн, влияя на их стабильность и распространение. Этот потенциал возникает из-за изменения метрики пространства, что приводит к модификации уравнения, описывающего динамику волн. В частности, положительная кривизна способствует стабилизации спиральных волн, препятствуя их распаду, в то время как отрицательная кривизна может приводить к их деформации или разрушению. Величина этого геометрического потенциала пропорциональна кривизне поверхности и играет ключевую роль в определении скорости и формы распространяющихся волн. Математически это проявляется в модификации $\nabla^2$ (лапласиана) на оператор Лапласа-Бельтрами, учитывающий геометрию пространства.

Оператор Лапласа-Бельтрами Δ представляет собой обобщение оператора Лапласа на римановы и псевдоримановы многообразия, позволяющее описывать диффузию и другие процессы, зависящие от градиента, на искривленных поверхностях. В отличие от стандартного оператора Лапласа, который применяется в евклидовом пространстве, оператор Лапласа-Бельтрами учитывает метрический тензор $g_{ij}$ поверхности, определяющий локальную геометрию. Формально, он определяется как $\Delta = \frac{1}{\sqrt{g}} \partial_i \left( \sqrt{g} g^{ij} \partial_j \right)$ , где $g$ — детерминант метрического тензора, а $g^{ij}$ — обратный метрический тензор. Это позволяет корректно моделировать распространение волн и другие диффузионные процессы на поверхностях сложной формы, где геометрия существенно влияет на динамику распространения.

При рассмотрении диффузии на искривленных поверхностях возникает понятие эффективной диффузии, которое отличается от классической диффузии в евклидовом пространстве. Это связано с тем, что геометрия поверхности влияет на движение частиц, изменяя их среднюю скорость и траектории. Эффективный коэффициент диффузии, обозначаемый как $D_{eff}$ , может отличаться от молекулярного коэффициента диффузии $D$ и зависит от кривизны поверхности. В частности, на поверхностях с положительной кривизной, $D_{eff}$ обычно уменьшается, замедляя распространение волн, а на поверхностях с отрицательной кривизной — увеличивается. Изменение скорости и формы распространяющихся волн, вызванное эффективной диффузией, играет ключевую роль в различных физических и биологических процессах, происходящих на искривленных пространствах.

Коническая геометрия, характеризующаяся высокой концентрацией кривизны в точке конуса, представляет собой предельный случай, наглядно демонстрирующий влияние геометрических факторов на динамику волн. В данной геометрии, даже незначительные возмущения могут приводить к значительным изменениям в амплитуде и форме распространяющейся волны. Это связано с тем, что $\nabla^2$ (оператор Лапласа-Бельтрами) в конической системе координат имеет сингулярность в вершине, что приводит к усилению или ослаблению волн в этой области. Экспериментальные и теоретические исследования показывают, что волны, приближаясь к вершине конуса, могут испытывать резкое изменение скорости и направления распространения, а также формировать сложные интерференционные картины, отличные от тех, что наблюдаются на плоских или слабоизогнутых поверхностях. Данный эффект имеет важное значение при моделировании распространения волн в различных физических системах, включая акустику, электромагнетизм и нейрофизиологию.

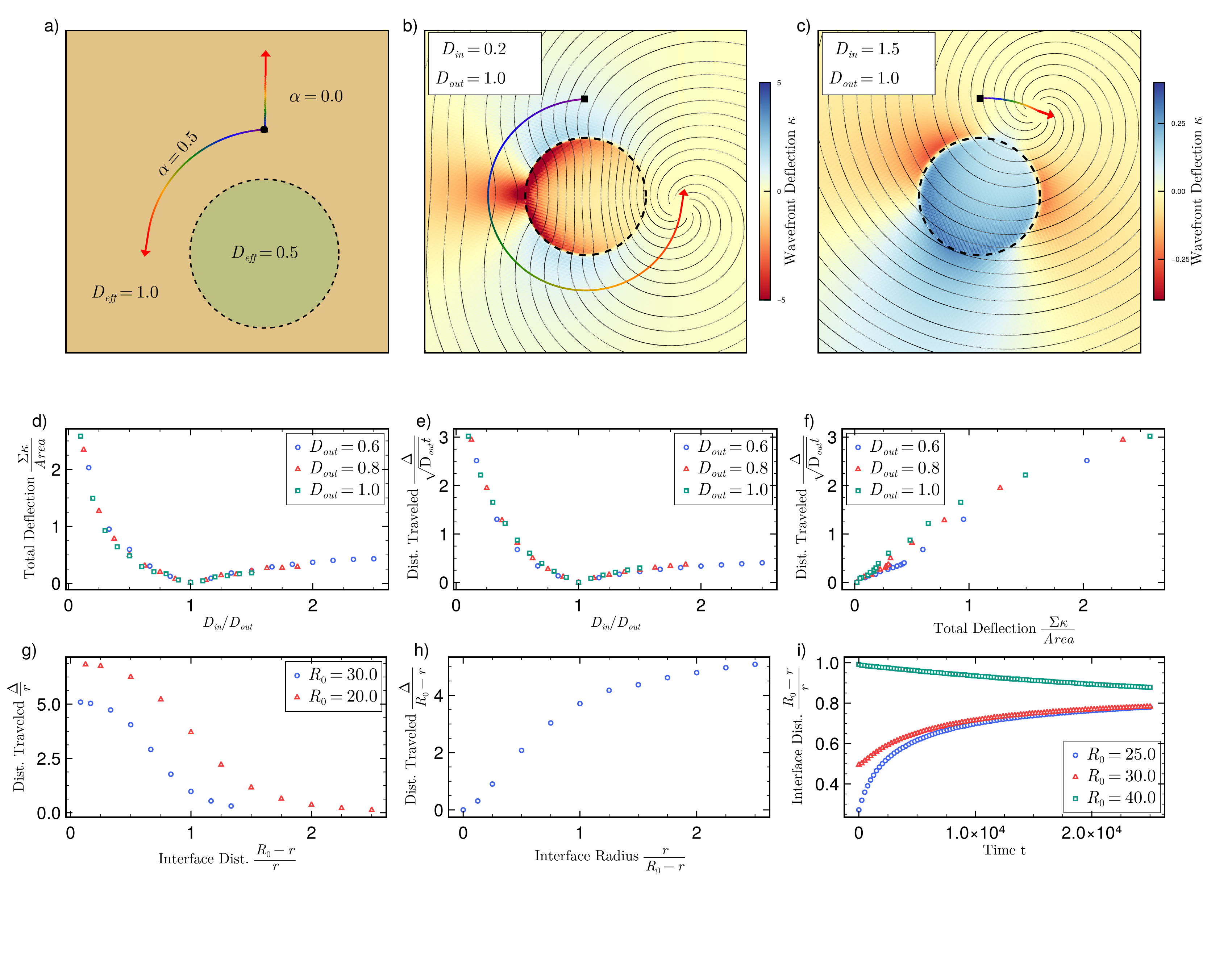
Пространственные градиенты коэффициента диффузии управляют движением дефектов на плоских поверхностях, заставляя их вращаться и перемещаться в зависимости от соотношения коэффициентов диффузии в центре и снаружи, при этом расстояние, пройденное дефектом, пропорционально этому соотношению и зависит от начального положения и размера области с пониженной диффузией.

Управление Волнами: Направляющие Геометрией

Отклонение фронтов волны, обусловленное градиентами эффективной диффузии, представляет собой механизм, посредством которого геометрия может управлять направлением распространения волны. Эффективная диффузия — это показатель скорости распространения волны в конкретной среде, и её неоднородность, создаваемая геометрическими особенностями, приводит к изменению траектории волны. Градиенты эффективной диффузии возникают из-за различий в свойствах среды, например, в плотности или проводимости, и заставляют волну отклоняться в сторону областей с более низкой диффузией. Величина отклонения пропорциональна крутизне градиента и скорости волны, что позволяет предсказывать и контролировать поведение волн в сложных геометрических конфигурациях. Этот принцип наблюдается в различных системах, включая распространение света в кристаллах и распространение звука в неоднородных средах.

Подвижность дефектов, являющаяся ключевым параметром, определяющим поведение волн в возбудимых средах, напрямую зависит от геометрической конфигурации среды. Изменение геометрии приводит к модификации локальных градиентов диффузии, что, в свою очередь, влияет на скорость и траекторию движения дефектов — точек, где волна временно прекращает распространение. В частности, сужение пространства или наличие препятствий увеличивает вероятность захвата дефектов, замедляя их движение и способствуя локализации волны. Напротив, расширение пространства или создание направляющих каналов может ускорить перемещение дефектов и поддерживать устойчивое распространение волны. $D = M \frac{kT}{6\pi\eta r}$ — коэффициент диффузии, где $M$ — подвижность, $k$ — постоянная Больцмана, $T$ — температура, η — вязкость, $r$ — радиус частицы, что демонстрирует прямую зависимость диффузии (и, следовательно, подвижности дефектов) от подвижности $M$ .

Геометрические собственные моды, возникающие в результате взаимодействия геометрии среды и динамики волн, выступают в роли организующих принципов для формирования спиральных волновых паттернов. Эти моды представляют собой устойчивые конфигурации волн, определяемые формой и границами области, в которой они распространяются. В частности, собственные значения и собственные функции, полученные из решения уравнения Гельмгольца в заданной геометрии, определяют частоты и пространственные характеристики этих мод. В результате, спиральные волны не являются случайными, а структурированы и упорядочены этими собственными модами, что позволяет предсказывать и контролировать их поведение. $\nabla^2 \psi + k^2 \psi = 0$ — уравнение Гельмгольца, описывающее волновые явления, где ψ — волновая функция, а $k$ — волновое число.

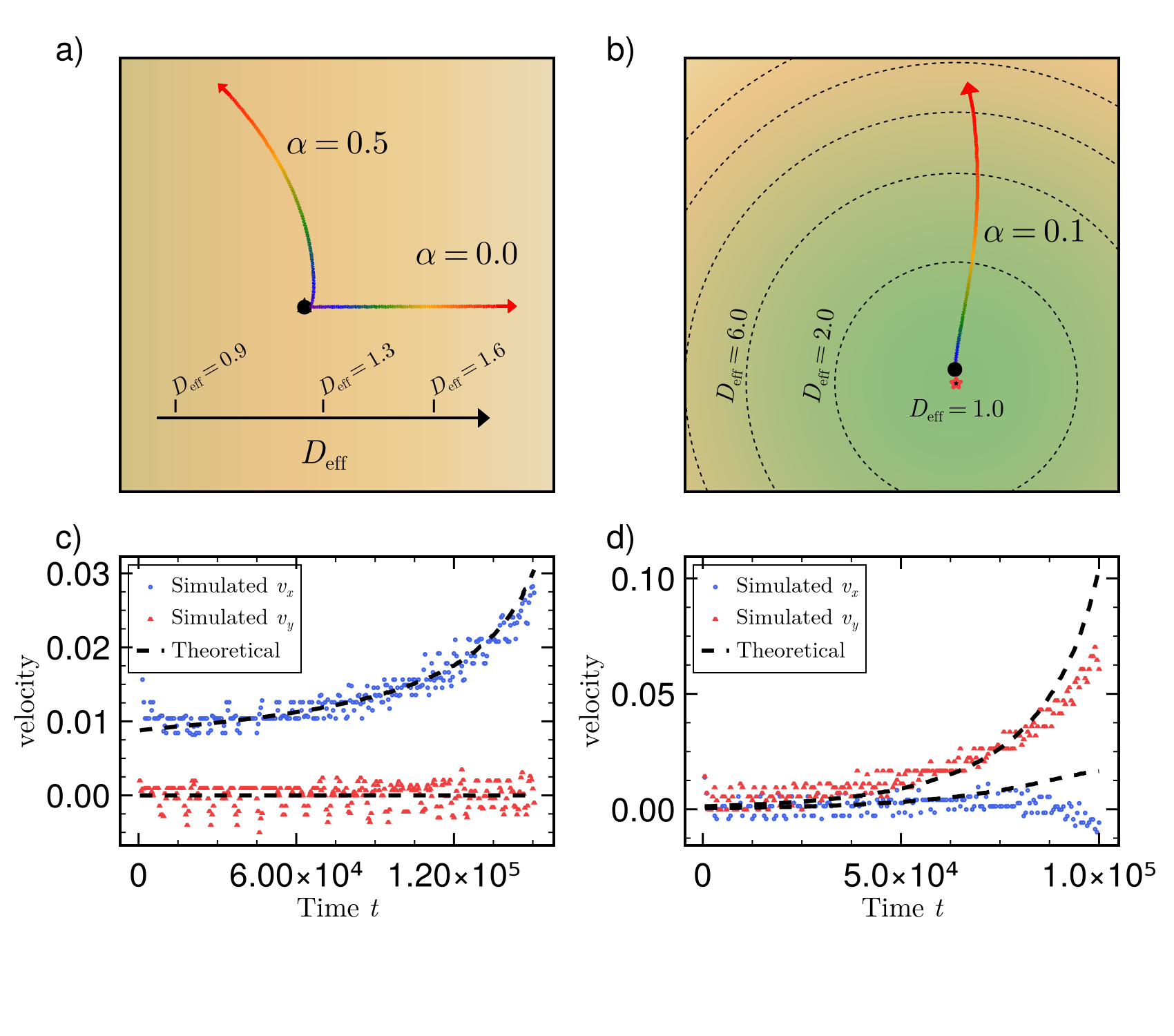
Понимание взаимодействия между геометрией и динамикой волн позволяет предположить, что биологические системы могут использовать геометрические особенности для выполнения конкретных функций. Например, спиральные волновые паттерны, возникающие в возбудимых клетках, могут быть организованы и направлены благодаря специфической геометрии ткани, что влияет на скорость и направление распространения сигналов. Аналогичные принципы могут лежать в основе формирования сложных структур и координации клеточных процессов, таких как развитие эмбриона или передача нервных импульсов, где геометрия играет ключевую роль в оптимизации функциональности и эффективности биологических систем.

Аналитические предсказания точно соответствуют результатам моделирования для градиентов эффективного коэффициента диффузии <span class="katex-eq" data-katex-display="false">DeffD_{\text{eff}}</span>, демонстрируя хорошее совпадение теоретических и численных скоростей как для линейного, так и для квадратичного градиентов при <span class="katex-eq" data-katex-display="false">\alpha=0</span> и <span class="katex-eq" data-katex-display="false">\alpha=0.1</span>. — Аналитические предсказания точно соответствуют результатам моделирования для градиентов эффективного коэффициента диффузии $DeffD_{\text{eff}}$ , демонстрируя хорошее совпадение теоретических и численных скоростей как для линейного, так и для квадратичного градиентов при $\alpha=0$ и $\alpha=0.1$ .

Биологическая Релевантность: От Слизевиков до Сердечной Ткани

Слизевики рода Dictyostelium используют спиральные волны цАМФ (циклического аденозинмонофосфата) для координированной агрегации клеток, что демонстрирует биологическую значимость этих паттернов. В условиях недостатка питательных веществ отдельные одноклеточные организмы начинают объединяться, формируя многоклеточную структуру. Этот процесс координируется посредством химических сигналов — волн цАМФ, распространяющихся по колонии. Спиральные волны обеспечивают эффективную передачу сигнала и направленное движение клеток к центру, где формируется многоклеточный организм, способный к миграции и размножению. Наблюдаемые спиральные паттерны свидетельствуют о наличии самоорганизующихся механизмов, позволяющих слизевикам эффективно реагировать на изменения окружающей среды и координировать коллективное поведение.

Кардиальные аритмии часто связаны с нарушениями спиральной динамики в сердечной ткани, что подчеркивает критическую важность стабильного распространения волн для нормальной физиологической функции. Нарушения в регулярности и скорости этих волн могут приводить к неэффективному сокращению сердечной мышцы и, как следствие, к аритмиям различной степени тяжести. Стабильная спиральная динамика обеспечивает координированное распространение электрических импульсов, необходимых для синхронного сокращения кардиомиоцитов и эффективного перекачивания крови. Нарушение этой стабильности, вызванное, например, гетерогенностью ткани или изменениями в ионных каналах, может приводить к формированию очагов реентри, поддерживающих аритмическую активность.

В коре головного мозга обнаружена спиралевидная волновая активность, что указывает на возможную роль этих паттернов в процессах нейронных вычислений и обработки информации. Данные волновые процессы, проявляющиеся как колебания электрической активности, могут служить основой для кодирования, передачи и интеграции сигналов между нейронами. Предполагается, что характеристики этих спиральных волн — скорость, амплитуда и траектория распространения — могут быть связаны с конкретными когнитивными функциями и процессами обучения. Исследования в данной области направлены на понимание того, как эти волновые паттерны способствуют формированию нейронных сетей и обработке информации в мозге.

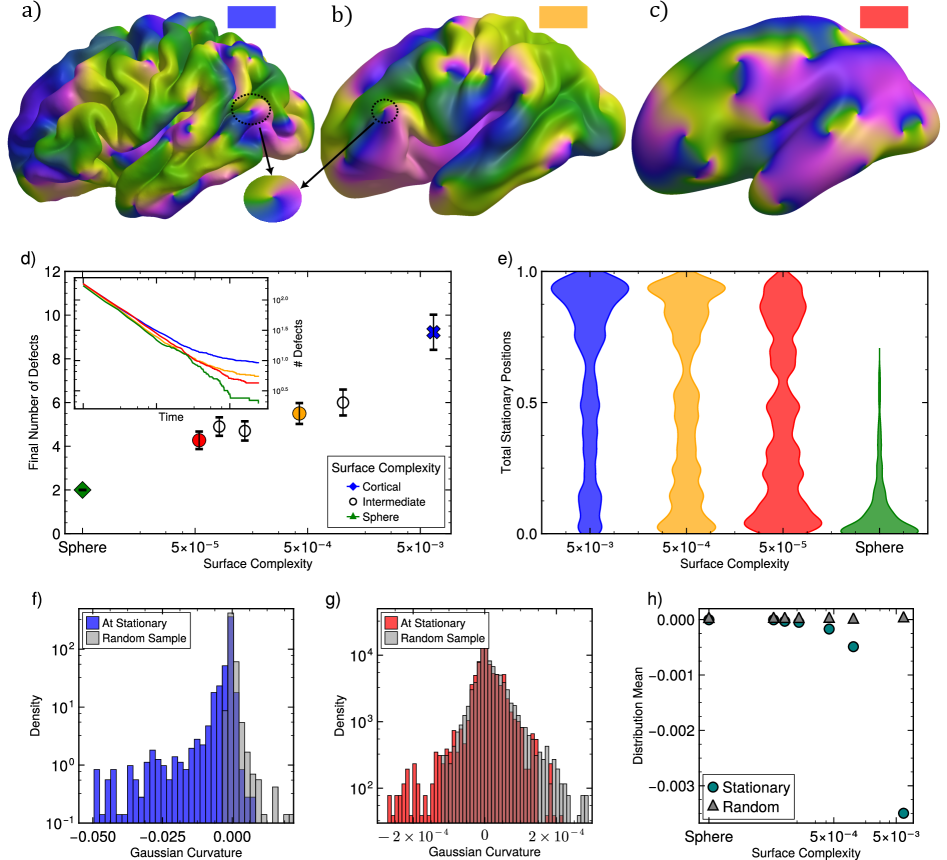
Исследования показали, что геометрия поверхности оказывает значительное влияние на динамику спиральных волн. В частности, реалистичные модели коры головного мозга демонстрируют значительно больше дефектов в распространении волн по сравнению со сферической поверхностью. В то время как на сфере наблюдалось снижение числа дефектов до минимального значения в 2, на моделях коры головного мозга сохранялось устойчивое количество дефектов на протяжении длительного времени, что указывает на более сложную и устойчивую структуру нарушений распространения волн.

Исследования показали, что дефекты, возникающие в спиральных волнах на поверхности коры головного мозга, демонстрируют значительно более высокую степень стационарности по сравнению с дефектами на сферической поверхности. В то время как на сфере дефекты преимущественно перемещаются, на поверхности коры более 90% времени они остаются неподвижными. Это различие в динамике дефектов указывает на влияние сложной геометрии коры на распространение волн и потенциально на лежащие в основе процессы обработки информации.

Анализ показывает, что средняя гауссова кривизна поверхности статистически смещена в сторону отрицательных значений в местах, где наблюдается стационарная локализация дефектов. Эта тенденция особенно выражена на более складчатых, сложных по геометрии поверхностях коры головного мозга. По сути, дефекты, фиксирующиеся на поверхности, предпочитают области с отрицательной гауссовой кривизной, что указывает на связь между локальной геометрией поверхности и динамикой спиральных волн. Данный факт предполагает, что геометрия коры может оказывать влияние на стабильность и распространение спиральных волн, играющих роль в нейронных процессах.

Теория ближнего поля успешно валидирована на конической геометрии посредством конформного отображения, позволяющего восстановить полный азимутальный угол и продемонстрировать соответствие аналитических и симулированных траекторий дефектов как для положительной, так и для отрицательной гауссовой кривизны, при этом точность соответствия сохраняется при низких значениях параметров.

Универсальный Принцип: Влияние на Вычисления и За Его Пределами

Взаимодействие между геометрией, диффузией и волновой динамикой представляет собой основополагающий принцип, управляющий самоорганизацией в самых разнообразных системах — от формирования узоров на поверхности жидкости до развития биологических структур и распространения информации в сложных сетях. Исследования показывают, что геометрия среды оказывает существенное влияние на процессы диффузии и распространения волн, определяя характер возникающих структур. Например, в системах с изменчивой кривизной, волны могут фокусироваться или рассеиваться, приводя к образованию сложных паттернов. Понимание этого взаимодействия позволяет предсказывать и контролировать процессы самоорганизации, открывая перспективы для создания новых материалов с заданными свойствами и разработки биовдохновленных вычислительных систем, использующих принципы самоорганизации для решения сложных задач. $\nabla^2 u = 0$ — уравнение, описывающее диффузию, тесно связано с геометрией пространства, в котором происходит процесс.

Использование изотермических координат представляет собой эффективный метод упрощения расчетов в системах с комплексной геометрией, особенно в случаях конических поверхностей. Традиционные системы координат часто сталкиваются с трудностями при описании таких форм, что усложняет моделирование диффузионных и волновых процессов. Изотермические координаты, в свою очередь, позволяют преобразовать сложную геометрию в эквивалентную плоскую, где вычисления значительно упрощаются. Это достигается за счет сохранения углов и конформного отображения, что критически важно для точного моделирования физических явлений. $\nabla^2$ оператор Лапласа, ключевой в уравнениях диффузии и волновых явлениях, приобретает более простую форму в изотермических координатах, облегчая решение этих уравнений и позволяя исследовать поведение систем в сложных геометрических условиях. Такой подход открывает возможности для разработки новых алгоритмов и моделей в различных областях науки, включая материаловедение и биологию.

Гауссова кривизна, представляющая собой меру локальной кривизны поверхности, играет ключевую роль в определении поведения волн, распространяющихся по ней. Исследования показывают, что волны не распространяются равномерно по всем поверхностям; их амплитуда и скорость существенно зависят от величины и знака гауссовой кривизны в каждой точке. Положительная гауссова кривизна, как, например, на поверхности сферы, приводит к фокусировке волн и увеличению их энергии, в то время как отрицательная кривизна, характерная для гиперболических поверхностей, вызывает рассеяние и уменьшение амплитуды. $K = \frac{1}{R_1R_2}$ , где $R_1$ и $R_2$ — главные радиусы кривизны, количественно определяет это влияние. Понимание этой взаимосвязи открывает возможности для создания материалов с заданными волновыми свойствами и разработки новых методов управления волнами в различных областях, от оптики и акустики до нейробиологии и материаловедения.

Исследования в области взаимодействия геометрии, диффузии и волновой динамики открывают перспективы для разработки принципиально новых подходов в различных областях науки и техники. В частности, принципы самоорганизации, лежащие в основе этих явлений, могут быть использованы для создания биовдохновленных вычислительных систем, имитирующих эффективность и адаптивность природных процессов. В материаловедении, понимание влияния кривизны поверхности на распространение волн позволит создавать материалы с заданными оптическими и механическими свойствами. Не менее перспективным представляется применение этих принципов в медицине, где управляемая волновая динамика может быть использована для разработки инновационных методов диагностики и терапии, например, для адресной доставки лекарств или стимуляции регенерации тканей. $\nabla^2 \phi = 0$ — уравнение Пуассона, описывающее многие из этих процессов, демонстрирует универсальность лежащих в основе закономерностей.

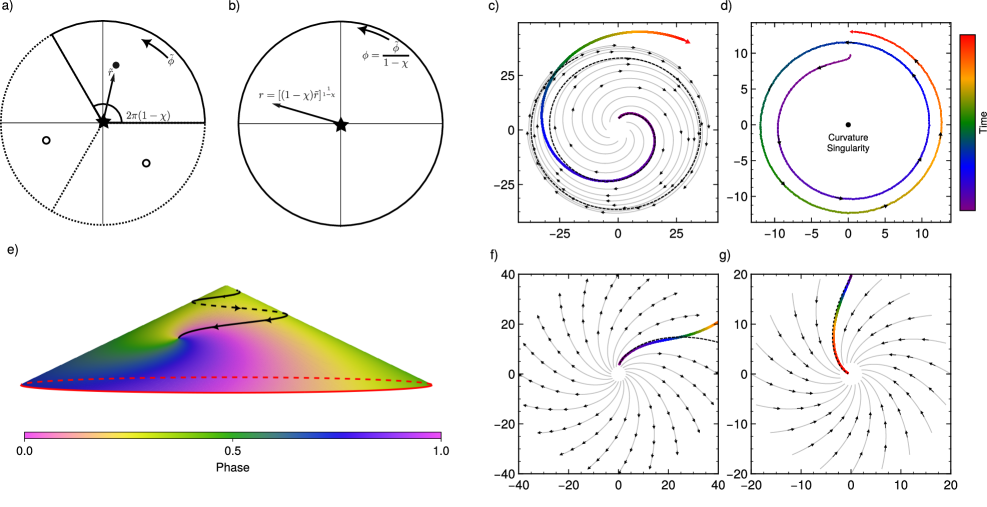
Исследование демонстрирует, как геометрия поверхности оказывает физическое воздействие на спиральные волны, направляя их динамику посредством эффективной диффузии. Это напоминает о сложности кажущихся простыми систем, где даже незначительные изменения в структуре могут привести к существенным последствиям. Стивен Хокинг однажды заметил: «Чем больше мы узнаем о Вселенной, тем сложнее она кажется». Эта фраза удивительно точно отражает суть представленной работы: изящное взаимодействие между кривизной поверхности и динамикой волн создает нетривиальные эффекты, способные, например, влиять на стабилизацию паттернов и пространственное распределение в нейронных сетях. Элегантность этого взаимодействия — признак глубокого понимания физических принципов, лежащих в основе подобных явлений.

Куда же дальше?

Исследование продемонстрировало, что кривизна поверхности — не просто геометрическая характеристика, но и реальная сила, воздействующая на спиральные волны. Элегантность этого открытия, однако, лишь подчеркивает глубину нерешенных вопросов. Необходимо признать, что предложенная модель эффективной диффузии, хотя и объясняет многие наблюдаемые явления, остается упрощением сложной реальности. В частности, влияние кривизны на волны в системах с неоднородными свойствами, где материал сам по себе обладает сложной структурой, требует дальнейшего изучения.

Очевидным направлением дальнейших исследований является расширение модели для учета нелинейных эффектов и взаимодействий между волнами. Как меняется динамика волн при высоких амплитудах? Как кривизна влияет на стабильность топологических дефектов? Эти вопросы требуют не только теоретических, но и экспериментальных решений. Особенно интересным представляется возможность применения полученных результатов к изучению нейронных сетей, где сложная геометрия мозга может играть ключевую роль в формировании и поддержании паттернов активности.

В конечном счете, истинная ценность этой работы заключается не в предоставлении готовых ответов, а в постановке новых, более сложных вопросов. Простое описание динамики спиральных волн на изогнутых поверхностях — лишь первый шаг. Понимание того, как эти волны формируют сложные структуры и влияют на функционирование сложных систем, — задача, требующая усилий многих поколений исследователей. И пусть эта задача будет нелегкой, ведь только в преодолении трудностей рождается истинное понимание.

Оригинал статьи: https://arxiv.org/pdf/2601.11321.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-01-19 20:25