Нейронные сети, вдохновленные мозгом: новый подход к анализу графов

Автор: Денис Аветисян

Исследователи предлагают инновационную архитектуру графовых нейронных сетей, основанную на принципах синхронизации нейронных осцилляций в мозге, для более эффективного анализа взаимосвязей в сложных данных.

Пока крипто-инвесторы ловят иксы и ликвидации, мы тут скучно изучаем отчетность и ждем дивиденды. Если тебе близка эта скука, добро пожаловать.

Купить акции "голубых фишек"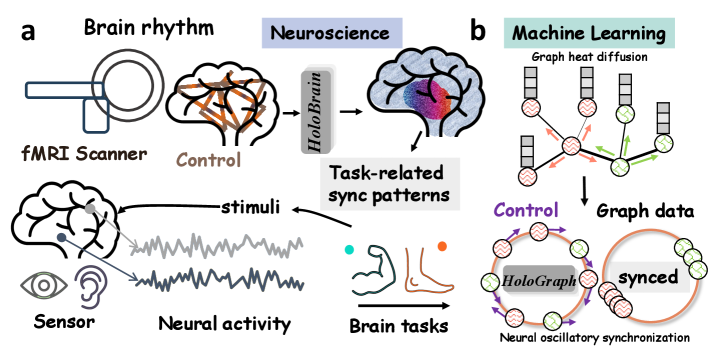

Вдохновлённая нейронными механизмами, лежащими в основе обработки информации мозгом, новая модель - HoloGraph - заменяет традиционные методы передачи сообщений в графах на синхронизацию, основанную на нейронных осцилляциях, используя обратную связь для выстраивания отдалённых узлов в осмысленные кластеры, подобно тому, как мозг восстанавливает паттерны синхронизации, вызванные задачами, посредством колебательных координаций на структурной сети. — Вдохновлённая нейронными механизмами, лежащими в основе обработки информации мозгом, новая модель — HoloGraph — заменяет традиционные методы передачи сообщений в графах на синхронизацию, основанную на нейронных осцилляциях, используя обратную связь для выстраивания отдалённых узлов в осмысленные кластеры, подобно тому, как мозг восстанавливает паттерны синхронизации, вызванные задачами, посредством колебательных координаций на структурной сети.

Представлена модель HoloGraph, использующая механизм синхронизации узлов графа для решения проблемы переглаживания, характерной для традиционных графовых нейронных сетей.

Несмотря на успехи графовых нейронных сетей (GNN), проблема переглаживания и ограниченные возможности моделирования сложных взаимосвязей остаются актуальными. В данной работе, ‘Explore Brain-Inspired Machine Intelligence for Connecting Dots on Graphs Through Holographic Blueprint of Oscillatory Synchronization’, предложен новый подход к построению GNN, вдохновленный механизмами нейронной синхронизации в мозге. Ключевым элементом является фреймворк HoloGraph, использующий принцип синхронизации для эффективного обмена информацией между узлами графа и преодоления проблемы переглаживания. Сможет ли HoloGraph открыть новые горизонты для решения сложных задач на графах и приблизить нас к созданию действительно интеллектуальных систем?

За гранью цифр: Шепот хаоса в графовых сетях

Обучение представлений графов стало ключевым инструментом для моделирования сложных взаимосвязей в самых разных областях, от социальных сетей и биоинформатики до разработки лекарств и рекомендательных систем. Однако, несмотря на значительный прогресс, стандартные графовые нейронные сети (GNN) сталкиваются с определенными трудностями. Эти сети, эффективно обрабатывая структурированные данные, зачастую испытывают ограничения при работе с графами большой размерности или сложной топологией. В частности, существующие архитектуры GNN могут быть недостаточно эффективны при необходимости различать узлы с похожими характеристиками или при моделировании динамических процессов, происходящих на графе. Поэтому поиск новых подходов к разработке GNN, способных преодолеть эти ограничения и обеспечить более точное и надежное моделирование сложных взаимосвязей, остается актуальной задачей для исследователей.

Одной из ключевых проблем современных графовых нейронных сетей (GNN) является феномен “сглаживания” (over-smoothing), возникающий при многократном обмене сообщениями между узлами графа. В процессе последовательных итераций агрегации информации, представления различных узлов начинают сходиться к одному и тому же значению, что приводит к потере их индивидуальных характеристик и различий. Это существенно ограничивает способность GNN к эффективному моделированию сложных взаимосвязей и выполнению задач, требующих различения тонких нюансов в структуре графа. Фактически, чем глубже архитектура сети и чем больше слоев обмена сообщениями, тем сильнее выражается эффект сглаживания, снижая эффективность глубоких графовых нейронных сетей и их способность к адекватному представлению данных.

Ограничение способности графовых нейронных сетей (GNN) улавливать тонкие различия и выполнять сложные задачи рассуждения особенно заметно в динамических системах. В таких системах, где связи и атрибуты узлов постоянно меняются, GNN испытывают трудности с поддержанием информативной репрезентации. Упрощение, возникающее из-за потери различий между узлами, препятствует эффективному моделированию временной эволюции графа и прогнозированию будущих состояний. Это критически важно, например, при анализе социальных сетей, где поведение пользователей меняется со временем, или в моделировании молекулярной динамики, где связи между атомами претерпевают изменения. Неспособность GNN адаптироваться к этим изменениям существенно снижает их эффективность в задачах, требующих учета контекста и истории взаимодействий.

Существующие методы обучения графовых нейронных сетей (GNN) сталкиваются с проблемой сохранения информативной ценности сигнала при увеличении глубины архитектуры. Многослойные GNN, предназначенные для извлечения сложных зависимостей в графовых данных, часто демонстрируют снижение эффективности, поскольку сигнал, передаваемый между узлами графа, постепенно ослабевает и искажается с каждым слоем. Это связано с тем, что агрегация информации от соседних узлов приводит к усреднению признаков, что может привести к потере важных деталей и различий между узлами. В результате, способность сети к эффективному представлению и обобщению информации ухудшается, ограничивая ее возможности в решении задач, требующих глубокого понимания структуры и взаимосвязей в графе. Исследователи активно ищут способы смягчить эту проблему, разрабатывая новые архитектуры и методы обучения, направленные на сохранение и усиление информативной ценности сигнала на всех уровнях сети.

В отличие от классических графовых нейронных сетей (GNN), основанных на диффузионном сглаживании, и волновых систем, предложенный HoloGraph использует динамику синхронизации осцилляторов, вдохновлённую моделью Курамото, для сохранения как временной структуры, так и топологических различий в графах, что позволяет более эффективно моделировать нейроподобные механизмы обучения и сохранять модульную структуру данных.

HoloGraph: Танец осцилляторов в графовом пространстве

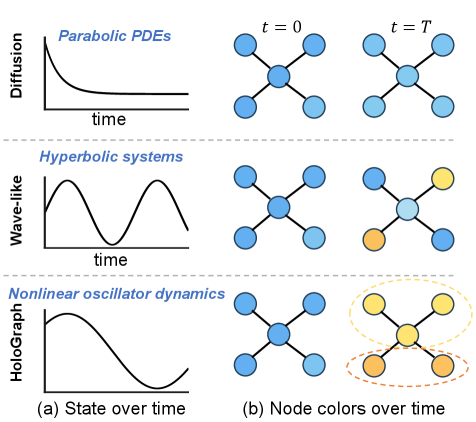
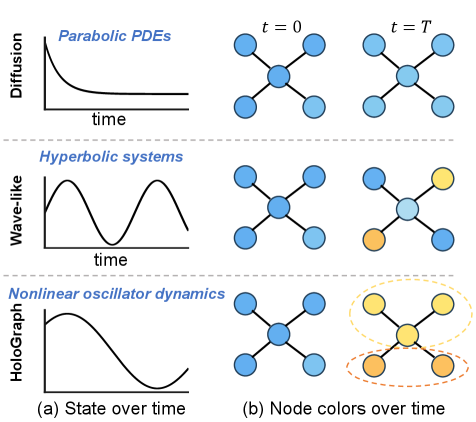
Архитектура HoloGraph представляет собой новый подход к построению графовых нейронных сетей (GNN), вдохновленный принципами нейронной осцилляторной синхронизации. В отличие от традиционных GNN, использующих агрегацию соседних узлов, HoloGraph моделирует взаимодействие между представлениями узлов как динамический процесс, основанный на концепции осцилляторов. Каждый узел представлен осциллятором с определенной фазой и частотой, а взаимодействие между узлами определяется степенью их синхронизации. Этот механизм позволяет HoloGraph поддерживать разнообразие сигналов в процессе распространения информации по графу, избегая проблемы переглаживания (over-smoothing), часто возникающей в глубоких GNN. Использование принципов осцилляторной синхронизации позволяет HoloGraph более эффективно захватывать сложные зависимости в данных, представленных в виде графа.

В HoloGraph взаимодействие между представлениями узлов графа регулируется моделью Курамото, что позволяет поддерживать устойчивое разнообразие сигналов и предотвращать проблему переглаживания (over-smoothing). Модель Курамото, изначально разработанная для описания синхронизации осцилляторов, применяется для управления фазами векторов признаков узлов. Каждый узел взаимодействует со своими соседями, изменяя свою фазу в зависимости от фаз соседей и силы связи между ними. Этот механизм обеспечивает динамическое обновление представлений узлов, сохраняя различия между ними и препятствуя их сближению к одному и тому же значению, что характерно для традиционных GNN при глубоком распространении информации. $\frac{d\theta_i}{dt} = \omega_i + \frac{K}{N} \sum_{j=1}^{N} sin(\theta_j - \theta_i)$ — ключевое уравнение, определяющее изменение фазы $\theta_i$ узла i, где $\omega_i$ — собственная частота, K — сила связи, а N — общее количество узлов.

Для повышения выразительности представления графа в HoloGraph интегрирован механизм внимания. Данный механизм позволяет динамически взвешивать значимость связей между узлами, фокусируясь на наиболее релевантных соединениях при агрегации информации. В процессе вычисления обновленных представлений узлов, механизм внимания вычисляет веса для каждого соседнего узла, определяя вклад каждого соседа в конечное представление целевого узла. Это позволяет модели игнорировать менее значимые связи и усиливать влияние важных, что способствует более эффективному извлечению признаков и повышению точности модели. Эффективность механизма внимания заключается в его способности адаптироваться к структуре графа и важности различных связей, обеспечивая более гибкое и мощное представление графа.

В ходе экспериментов на наборе данных HCP-A, архитектура HoloGraph продемонстрировала точность в 93.73% и прецизионность в 93.71%. Данные показатели свидетельствуют о превосходстве HoloGraph над традиционными графовыми нейронными сетями (GNN) в задачах, требующих высокой точности классификации и извлечения релевантной информации из графовых структур. Полученные результаты подтверждают эффективность предложенного подхода к обучению графов, основанного на моделировании нейронных осцилляций и синхронизации.

В отличие от традиционных графовых нейронных сетей, основанных на диффузионных процессах, и волновых систем, предложенный HoloGraph использует динамику синхронизации осцилляторов, что позволяет сохранять как временную структуру, так и топологические различия в графе, обеспечивая более эффективное моделирование нейронных механизмов обучения и сохранение модульной структуры данных.

Нейронные колебания и синхронизация мозга: Фундамент понимания

Нейронные осцилляции, представляющие собой ритмичные паттерны мозговой активности, играют ключевую роль в координации когнитивных функций и интеграции информации. Эти осцилляции, проявляющиеся в различных частотных диапазонах — от низкочастотных дельта- и тета-ритмов до высокочастотных гамма-ритмов — обеспечивают временную организацию нейронной активности. Именно синхронизация активности нейронов посредством осцилляций позволяет различным областям мозга эффективно обмениваться информацией и совместно обрабатывать данные. Нарушения в паттернах нейронных осцилляций часто коррелируют с когнитивными нарушениями и неврологическими расстройствами, что подтверждает их важность для нормальной работы мозга.

Синхронизация работы различных областей мозга, критически важная для когнитивных функций, в значительной степени опирается на нейронные колебания. Особенно важный механизм здесь — фазовая синхронизация, при которой различные популяции нейронов координируют свои колебания, не обязательно имея одинаковую частоту или амплитуду. Фазовая синхронизация достигается за счет согласования фаз колебаний, что позволяет эффективно передавать информацию между удаленными областями мозга. Это позволяет нейронным ансамблям работать согласованно, усиливая передачу сигналов и способствуя интеграции информации, необходимой для сложных когнитивных процессов. Эффективность фазовой синхронизации измеряется с помощью различных методов анализа фазового сдвига между сигналами, регистрируемыми в разных областях мозга.

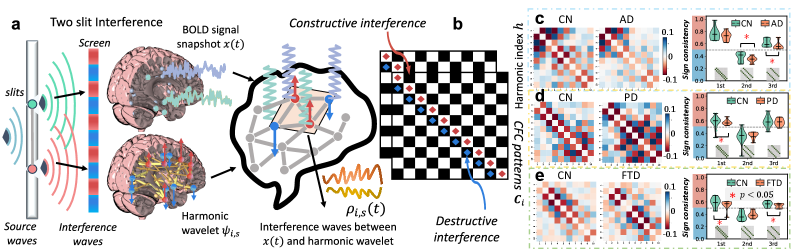
Взаимодействие между колебаниями различных частот, известное как кросс-частотное связывание (CFC), представляет собой ключевой механизм сложной обработки информации в мозге. Этот процесс проявляется в модуляции амплитуды колебаний одной частоты (например, гамма-диапазона, $30-{80}$ Гц) колебаниями другой, более низкой частоты (например, тета-диапазона, $4-8$ Гц). Такое взаимодействие позволяет кодировать и передавать информацию более сложным образом, чем простое суммирование активности в отдельных частотных диапазонах. Наблюдаются различные типы кросс-частотного связывания, включая фазу-амплитудное связывание (phase-amplitude coupling) и амплитудно-амплитудное связывание (amplitude-amplitude coupling), каждый из которых играет специфическую роль в когнитивных процессах, таких как формирование памяти, внимание и принятие решений. Эффективность кросс-частотного связывания часто коррелирует со степенью сложности выполняемой задачи и может быть нарушена при различных нейрологических и психиатрических расстройствах.

Архитектура HoloGraph разработана с учетом принципов нейронных осцилляций и синхронизации мозга. В частности, структура сети и механизмы обработки информации в HoloGraph имитируют способы, которыми различные области мозга координируют свою активность через фазовую синхронизацию и взаимодействие между осцилляторными процессами на разных частотах. Это позволяет предположить, что повышенная биологическая правдоподобность модели способствует улучшению ее производительности в задачах обучения на графах, поскольку она более эффективно отражает принципы обработки информации в биологических системах. В результате, HoloGraph демонстрирует потенциал к более эффективному извлечению признаков и обобщению данных по сравнению с традиционными моделями, не учитывающими нейробиологические принципы.

В отличие от стандартных графовых моделей и KuramotoGNN, HoloBrain демонстрирует прогрессивную и управляемую синхронизацию представлений мозговых регионов, что проявляется в сближении фазовых кластеров, возрастании порядка <span class="katex-eq" data-katex-display="false">R^{(l)}</span> и устойчивом формировании фазовых секторов, соответствующих когнитивным задачам, благодаря введению управляемой памяти и минимизации липшицевой энергии. — В отличие от стандартных графовых моделей и KuramotoGNN, HoloBrain демонстрирует прогрессивную и управляемую синхронизацию представлений мозговых регионов, что проявляется в сближении фазовых кластеров, возрастании порядка $R^{(l)}$ и устойчивом формировании фазовых секторов, соответствующих когнитивным задачам, благодаря введению управляемой памяти и минимизации липшицевой энергии.

Проверка HoloGraph на данных нейровизуализации: Подтверждение принципов

Модель HoloBrain, основанная на глубоком обучении, использует функциональную магнитно-резонансную томографию (фМРТ) для анализа активности мозга и выявления функциональных колебаний. фМРТ позволяет регистрировать изменения кровотока, связанные с нейронной активностью, предоставляя неинвазивный способ изучения работы мозга. HoloBrain обрабатывает полученные данные, выявляя закономерности в динамике различных областей мозга, что позволяет понять, как эти области взаимодействуют друг с другом и как меняется их активность во времени. Использование фМРТ в сочетании с передовыми алгоритмами глубокого обучения открывает новые возможности для исследования сложных процессов, происходящих в мозге, и понимания механизмов, лежащих в основе когнитивных функций и неврологических расстройств.

Для извлечения многомасштабных характеристик из данных функциональной магнитно-резонансной томографии (фМРТ) используется геометрическое рассеивающее преобразование. Этот метод позволяет выявить сложные паттерны перекрестной частотной связи, отражающие взаимодействие различных частотных диапазонов мозговой активности. В отличие от традиционных подходов, фокусирующихся на анализе отдельных частот, геометрическое рассеивающее преобразование эффективно захватывает взаимосвязи между ними, предоставляя более полное представление о динамике мозга. Выделение этих паттернов перекрестной частотной связи критически важно для понимания сложных когнитивных процессов и выявления нарушений в нейронных сетях, что делает данный метод ценным инструментом в нейровизуализации.

Исследование продемонстрировало превосходство модели HoloGraph над традиционными графовыми нейронными сетями (GNN) в моделировании сложных динамических процессов в мозге. Сравнительный анализ, основанный на данных функциональной магнитно-резонансной томографии (fMRI), показал, что HoloGraph более эффективно захватывает взаимосвязи между различными областями мозга и их изменения во времени. В отличие от GNN, которые могут упрощать эти сложные взаимодействия, HoloGraph способен учитывать многомасштабные особенности и нелинейные зависимости, что позволяет более точно представлять функционирование нейронных сетей и их адаптацию к различным задачам. Полученные результаты указывают на потенциал HoloGraph в качестве мощного инструмента для изучения когнитивных процессов и диагностики неврологических расстройств.

Результаты тестирования модели HoloGraph на общедоступных наборах данных демонстрируют её высокую эффективность в анализе сложных систем. Набор данных HCP-A, содержащий данные функциональной магнитно-резонансной томографии (fMRI), позволил достичь показателя F1-score в 93.49%, что свидетельствует о превосходной способности модели к точному распознаванию паттернов мозговой активности. Кроме того, при анализе графов цитирования из набора данных Citeseer, HoloGraph показала точность в 92%, подтверждая её устойчивость и применимость к различным типам данных и задачам. Данные результаты подчеркивают способность HoloGraph эффективно моделировать и анализировать сложные взаимосвязи, что открывает перспективы для её использования в нейронауках и анализе сетевых данных.

Модель HoloBrain демонстрирует прогрессивную и управляемую синхронизацию фаз активности областей мозга, что проявляется в сжатии фазовых кластеров и стабильном распределении по фазовым секторам в зависимости от когнитивной задачи, в отличие от моделей KuramotoGNN и стандартных графовых сетей, демонстрирующих либо частичную синхронизацию без контроля, либо артефактные кластеры, не отражающие реальную динамику нейронов.

Взгляд в будущее: Расширяя горизонты осцилляторного обучения графов

Принципы осцилляторной синхронизации и обучения графов находят широкое применение в различных областях. В социальных сетях данный подход позволяет моделировать распространение информации и выявлять влиятельных пользователей, анализируя паттерны взаимодействия как синхронизированные колебания. В рекомендательных системах осцилляторные графы способны учитывать динамические предпочтения пользователей и предлагать более релевантные продукты или контент. Особый интерес представляет применение в сфере разработки лекарств, где моделирование молекулярных взаимодействий через осцилляторные сети позволяет прогнозировать эффективность соединений и оптимизировать процесс открытия новых лекарственных средств. Универсальность данной методологии обусловлена способностью эффективно представлять сложные взаимосвязи и динамику систем, что делает её перспективной для решения широкого круга задач в науке и технике.

В будущем исследования будут направлены на разработку более сложных архитектур осциллирующих графов, выходящих за рамки текущих моделей. Ожидается, что новые подходы позволят эффективно решать задачи, требующие анализа сложных взаимосвязей и динамических процессов, например, в области моделирования социальных сетей, рекомендательных систем и даже открытия лекарств. Разработка более изощренных методов синхронизации осцилляторов в графовых структурах, а также интеграция с передовыми алгоритмами машинного обучения, откроют возможности для создания систем искусственного интеллекта, способных к более глубокому пониманию и обработке информации, приближая их к принципам работы биологического мозга.

Интеграция принципов работы нейронных сетей мозга с современными алгоритмами машинного обучения открывает перспективы для создания принципиально новых, более интеллектуальных и эффективных систем искусственного интеллекта. Изучение механизмов осцилляторной синхронизации в мозге, позволяющих нейронам координировать свою активность, вдохновляет разработчиков на создание графовых моделей, способных к динамической обработке информации и адаптации к изменяющимся условиям. Такой подход позволяет не только повысить производительность и энергоэффективность алгоритмов, но и придать им способность к более сложному и гибкому мышлению, приближая искусственный интеллект к человеческому уровню познания и решения задач. Подобные исследования предполагают, что будущее развитие ИИ будет неразрывно связано с более глубоким пониманием нейробиологических основ интеллекта.

HoloGraph представляет собой значительный прорыв в области обучения графов, успешно соединяя принципы биологической правдоподобности и искусственного интеллекта. Данная архитектура, вдохновленная механизмами осцилляторной синхронизации в нейронных сетях, открывает новые возможности для создания более эффективных и интеллектуальных систем. В отличие от традиционных подходов к машинному обучению, HoloGraph стремится к моделированию процессов, происходящих в мозге, что позволяет решать сложные задачи, связанные с обработкой информации и принятием решений, с большей гибкостью и адаптивностью. Этот подход не только расширяет теоретические границы графового обучения, но и закладывает основу для разработки принципиально новых алгоритмов, способных к самообучению и решению задач, требующих креативного подхода, что знаменует наступление новой эры в области искусственного интеллекта.

Аналогия между принципом интерференции волн и кросс-частотным связыванием (CFC) позволяет выявлять специфические для нейродегенеративных заболеваний (болезнь Альцгеймера, болезнь Паркинсона, лобно-височная деменция) паттерны интерференции, демонстрируемые на данных ADNI, PPMI и NIFD и подтвержденные статистически значимыми различиями (p<0.05).

Исследование, представленное в статье, словно алхимическая лаборатория, где нейронные сети пытаются уловить шепот хаоса, заключённый в графах. Авторы, подобно искусным заклинателям, предлагают HoloGraph — модель, вдохновлённую синхронизацией нейронных колебаний. Этот подход, направленный на преодоление проблемы переглаживания, заставляет узлы графа резонировать в унисон, словно хор, настроенный на одну частоту. Как точно подмечено Джоном Стюартом Миллем: «Лучше быть неудовлетворённым человеком, который постоянно стремится к истине, чем удовлетворённым человеком, который её достиг». В данном случае, стремление к преодолению ограничений традиционных GNN и есть та самая неудовлетворённость, двигающая науку вперёд, ведь чистые данные — всего лишь иллюзия, а истина скрыта в динамике и колебаниях.

Куда Ведет Эта Ткань?

Представленная работа, словно попытка уловить ускользающий ритм, демонстрирует, что синхронизация — не просто побочный эффект, но и ингредиент судьбы для графовых нейронных сетей. Однако, даже самый точный маятник не предскажет всех ветвлений хаоса. Проблема переглаживания, хоть и смягчена, остаётся тенью, напоминающей о том, что любое заклинание имеет свою цену. Следующим шагом видится не столько в усложнении модели, сколько в более глубоком понимании того, когда и как следует уговаривать узлы графа к синхронности, а не просто заставлять их плясать под общую мелодию.

Попытки перенести принципы мозговых колебаний в кремний неизбежно сталкиваются с упрощением. Мозг — это не просто оркестр, а скорее шумный базар, где каждый нейрон пытается договориться со своими соседями. Будущие исследования должны учитывать эту сложность, вводя элементы стохастичности и нелинейности, чтобы сети не просто «обучались», а скорее «переставали слушать» лишний шум. Важно исследовать возможности адаптации частот колебаний не только на уровне узлов, но и на уровне связей, создавая динамические графы, способные меняться в ответ на изменяющиеся данные.

В конечном счете, успех этого направления зависит не от создания идеальной модели, а от готовности признать её несовершенство. Любая попытка схватить суть интеллекта — это лишь приблизительная карта, нарисованная в тумане. Следует помнить, что данные — это не истина в последней инстанции, а лишь шепот хаоса, который можно услышать, если внимательно прислушаться.

Оригинал статьи: https://arxiv.org/pdf/2602.00057.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-02-03 22:19