Восстановление фазы в дифракционных изображениях: новый взгляд с помощью Vision Transformer

Автор: Денис Аветисян

Исследователи предлагают инновационный подход к восстановлению фазы в когерентной дифракционной визуализации, используя архитектуру Vision Transformer для анализа сложных многодоменных кристаллов.

Пока крипто-инвесторы ловят иксы и ликвидации, мы тут скучно изучаем отчетность и ждем дивиденды. Если тебе близка эта скука, добро пожаловать.

Купить акции "голубых фишек"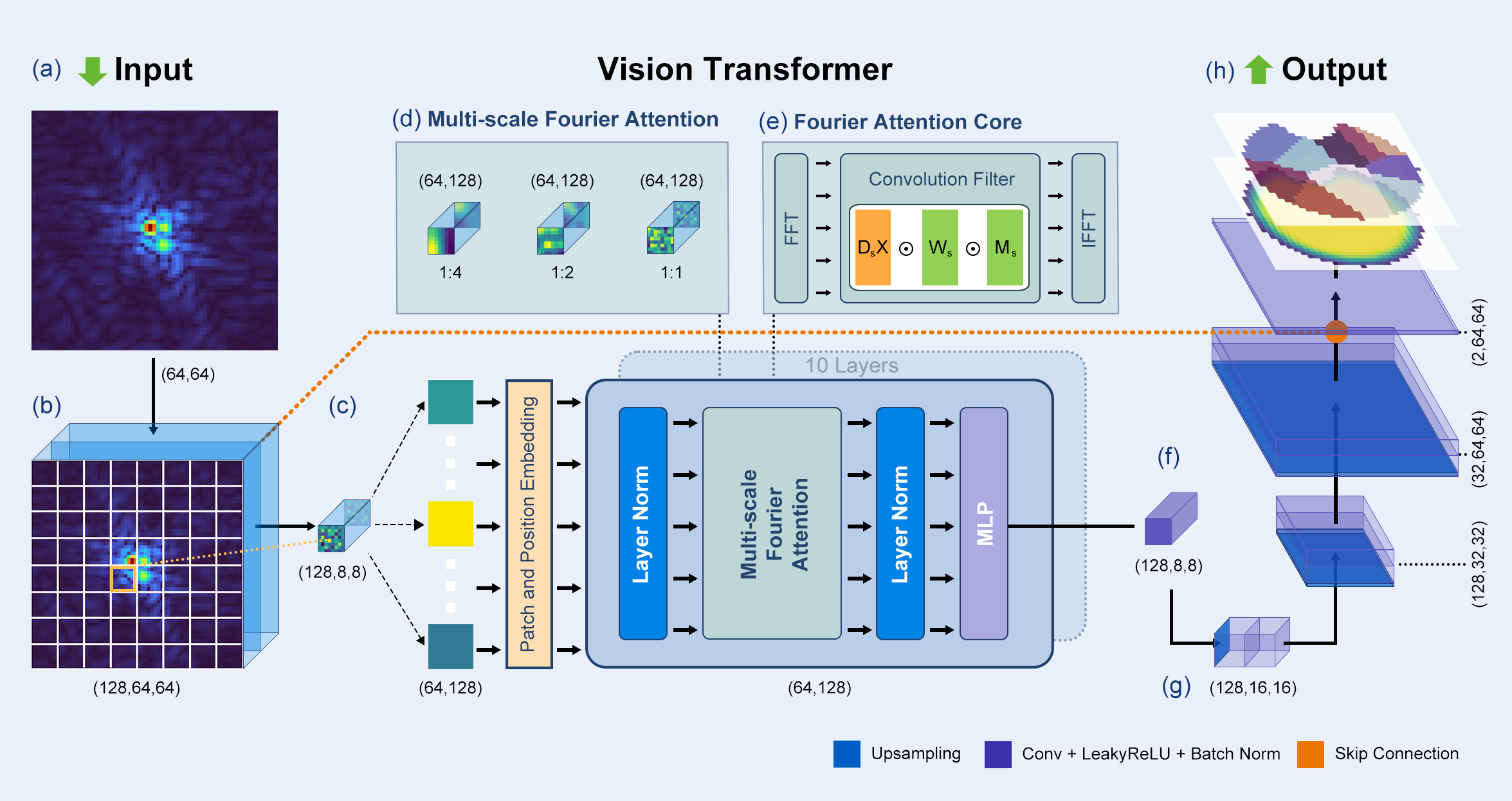

Модель Fourier ViT, предназначенная для восстановления фазы дифракции, обрабатывает входные данные размером 64x64, извлекая признаки с помощью неглубокой свёрточной сети и разделяя изображение на патчи размером 16x16 для формирования последовательности токенов, которые затем обрабатываются многослойным Vision Transformer с многомасштабным Фурье-вниманием и глобальной свёрткой на основе FFT, что позволяет реконструировать комплексное кристаллическое поле и получить карты амплитуды и фазы в реальном пространстве, согласующиеся с измеренной дифракционной картиной. — Модель Fourier ViT, предназначенная для восстановления фазы дифракции, обрабатывает входные данные размером 64×64, извлекая признаки с помощью неглубокой свёрточной сети и разделяя изображение на патчи размером 16×16 для формирования последовательности токенов, которые затем обрабатываются многослойным Vision Transformer с многомасштабным Фурье-вниманием и глобальной свёрткой на основе FFT, что позволяет реконструировать комплексное кристаллическое поле и получить карты амплитуды и фазы в реальном пространстве, согласующиеся с измеренной дифракционной картиной.

В работе представлен Fourier Vision Transformer для эффективного восстановления фазы в Bragg Coherent Diffraction Imaging, решающий проблему сильной фазы для многодоменных кристаллов.

Восстановление фазы в дифракционных изображениях становится все более сложной задачей при наличии значительных деформаций кристаллической решетки, особенно в случае многодоменных структур. В данной работе, посвященной ‘Vision Transformer for Multi-Domain Phase Retrieval in Coherent Diffraction Imaging’, предложен новый подход, основанный на использовании архитектуры Fourier Vision Transformer (ViT) для решения проблемы восстановления фазы в когерентной дифракционной визуализации. Разработанный метод эффективно решает задачу восстановления фазы для многодоменных кристаллов с сильными фазовыми контрастами, используя механизм внимания, работающий в частотной области, и демонстрирует превосходство над традиционными итеративными алгоритмами и сверточными нейронными сетями. Сможет ли предложенный подход стать стандартом для анализа сложных кристаллических структур и открыть новые возможности в материаловедении и нанотехнологиях?

Раскрытие Скрытых Структур: Брэгговская Когерентная Дифракция

Брэгговская когерентная дифракционная визуализация (БКДИ) представляет собой мощный метод, позволяющий исследовать трёхмерную структуру материалов на наноуровне без использования линз. В отличие от традиционной микроскопии, БКДИ формирует изображение на основе анализа дифракционной картины, возникающей при облучении образца когерентным рентгеновским излучением. Однако, получение детального изображения требует применения сложных вычислительных алгоритмов, поскольку информация о фазе волны, потерянная при регистрации дифракционной картины, должна быть восстановлена. Этот процесс, известный как фазовая реконструкция, является ключевым этапом в БКДИ и требует значительных вычислительных ресурсов и разработки эффективных алгоритмов для обработки данных и получения высококачественных изображений наноструктур.

В основе метода Брэгговской когерентной дифракции лежит сложная задача восстановления фазы — реконструкция изображения объекта по его дифракционной картине. Эта задача является принципиально некорректной, поскольку бесконечному числу исходных объектов может соответствовать один и тот же наблюдаемый дифракционный узор. По сути, информация о фазе, необходимой для формирования полного изображения, теряется в процессе дифракции, и ее приходится восстанавливать на основе математических алгоритмов и априорных ограничений. Неоднозначность решения требует использования сложных итеративных методов, которые стремятся найти наиболее вероятное решение, соответствующее физическим свойствам исследуемого материала. Успешное решение этой проблемы является ключевым для получения высококачественных трехмерных изображений на наноуровне, однако требует значительных вычислительных ресурсов и разработки усовершенствованных алгоритмов восстановления фазы.

Традиционные итеративные алгоритмы восстановления фазы, такие как методы Герчберга-Сакстона и гибридного ввода-вывода, демонстрируют свою эффективность при анализе относительно простых структур. Однако, при работе со сложными образцами, содержащими множество рассеивающих элементов, или при наличии значительного шума в дифракционной картине, их возможности существенно ограничены. Эти алгоритмы часто сталкиваются с проблемой сходимости — они могут застревать в локальных минимумах, приводя к неверному или размытому изображению. Сложность заключается в том, что дифракционная картина содержит информацию лишь об амплитуде рассеянных волн, а фаза, определяющая пространственное распределение рассеивающих центров, теряется в процессе измерения. Восстановление фазы требует использования дополнительных ограничений и предположений, и традиционные методы оказываются недостаточно устойчивыми к неточностям и помехам, возникающим при анализе реальных наноструктур.

Сравнительное исследование методов фазовой реконструкции на экспериментальных данных нанокристалла LCMO-500 показало, что итеративный метод, Fourier ViT и C-CNN позволяют восстановить амплитуду и фазу кристалла, при этом анализ гистограмм <span class="katex-eq" data-katex-display="false">\chi^{2}</span> (диапазон 0.0% - 2.0%) позволяет оценить качество реконструкции. — Сравнительное исследование методов фазовой реконструкции на экспериментальных данных нанокристалла LCMO-500 показало, что итеративный метод, Fourier ViT и C-CNN позволяют восстановить амплитуду и фазу кристалла, при этом анализ гистограмм $\chi^{2}$ (диапазон 0.0% — 2.0%) позволяет оценить качество реконструкции.

Трансформеры для Восстановления Фазы: Новый Подход

В рамках восстановления фазы методом дифракции обратного пространства (BCDI) предложена адаптация архитектуры Vision Transformer (ViT), изначально разработанной для задач компьютерного зрения. ViT представляет собой глубокую нейронную сеть, основанную на механизме самовнимания, позволяющем обрабатывать данные как последовательность «патчей» — фрагментов изображения. В отличие от традиционных сверточных нейронных сетей (CNN), ViT не требует жесткой локальной связности между пикселями, что позволяет эффективно улавливать глобальные зависимости в дифракционной картине и использовать преимущества параллельных вычислений. Адаптация ViT для BCDI позволяет обрабатывать данные, полученные в результате дифракции, как последовательность фрагментов в частотном пространстве, что обеспечивает возможность восстановления фазы и реконструкции структуры образца.

Ключевым нововведением в Vision Transformer (ViT) для задач восстановления фазы является механизм ‘FourierAttention’. Он позволяет эффективно обрабатывать данные, представленные в пространстве Фурье — критически важную область для анализа дифракционных картин. В отличие от традиционных сверточных нейронных сетей, FourierAttention оперирует непосредственно с данными в частотной области, что позволяет учитывать глобальные зависимости между различными частотными компонентами. Это обеспечивает более эффективное использование информации о структуре образца, закодированной в дифракционной картине, и позволяет модели более точно восстанавливать фазу и, следовательно, структуру объекта. Эффективность достигается за счет использования принципов внимания (attention), которые позволяют модели концентрироваться на наиболее релевантных частотных компонентах при реконструкции изображения.

В отличие от традиционных сверточных нейронных сетей (CNN), которые обрабатывают данные локально, Vision Transformer (ViT) устанавливает долгосрочные зависимости внутри дифракционных данных. CNN используют локальные фильтры, что ограничивает их способность учитывать глобальный контекст структуры. ViT, применяя механизм внимания (attention), способен анализировать взаимосвязи между любыми двумя точками в дифракционной картине, независимо от их расстояния. Это позволяет модели учитывать глобальную структуру объекта, что критически важно для точной реконструкции, особенно в случаях сложных образцов или при наличии шума. Таким образом, ViT эффективно захватывает информацию о структуре, которая может быть упущена локальными операциями свертки.

Восстановление фазы с использованием Vision Transformer (ViT) демонстрирует высокую устойчивость к шумам и позволяет эффективно реконструировать структуры даже при наличии сложных образцов. В отличие от традиционных методов, ViT способен корректно обрабатывать дифракционные картины, искаженные шумом, благодаря механизму FourierAttention и способности устанавливать долгосрочные зависимости между различными участками данных. Это обеспечивает более точное определение фазы и, следовательно, более качественную реконструкцию структуры образца, даже в условиях низкой SNR. Устойчивость к сложным структурам обеспечивается за счет глобального анализа данных дифракции, что позволяет ViT учитывать взаимосвязи между всеми точками данных, а не только локальные особенности.

Модель Fourier ViT успешно реконструирует синтетический кристалл из дифракционной картины, демонстрируя соответствие между истинным и реконструированным профилями дифракции и низкое значение <span class="katex-eq" data-katex-display="false">\chi^{2}</span> для восстановления как амплитуды, так и фазы кристалла. — Модель Fourier ViT успешно реконструирует синтетический кристалл из дифракционной картины, демонстрируя соответствие между истинным и реконструированным профилями дифракции и низкое значение $\chi^{2}$ для восстановления как амплитуды, так и фазы кристалла.

Учет Сложностей: Многодоменные Кристаллы и Шум

Реальные образцы кристаллических структур часто демонстрируют полидоменное строение, характеризующееся вариациями в ориентации и составе отдельных доменов. Данное явление значительно усложняет задачу фазовой реконструкции, поскольку традиционные алгоритмы, предполагающие однородность кристаллической решетки, становятся менее эффективными. Различия в ориентации доменов приводят к интерференционным эффектам, искажающим полученное изображение, а вариации в составе влияют на рассеяние рентгеновских лучей или электронов, что также затрудняет точную реконструкцию фазы. Неоднородность структуры требует применения более сложных алгоритмов и методов обработки данных для корректного восстановления исходной информации о кристалле.

Для моделирования сложных структур многодоменных кристаллов в наших исследованиях используется метод диаграммы Вороного (Voronoi Diagram). Этот подход позволяет генерировать синтетические образцы, имитирующие реалистичные вариации в ориентации и составе кристаллических доменов. Диаграмма Вороного эффективно разбивает пространство на ячейки, соответствующие различным кристаллическим ориентациям, что позволяет контролировать количество доменов, их размер и взаимное расположение. Полученные синтетические данные служат основой для тестирования и валидации алгоритмов фазовой реконструкции в условиях, приближенных к реальным экспериментальным данным, и позволяют оценить их устойчивость к структурным неоднородностям.

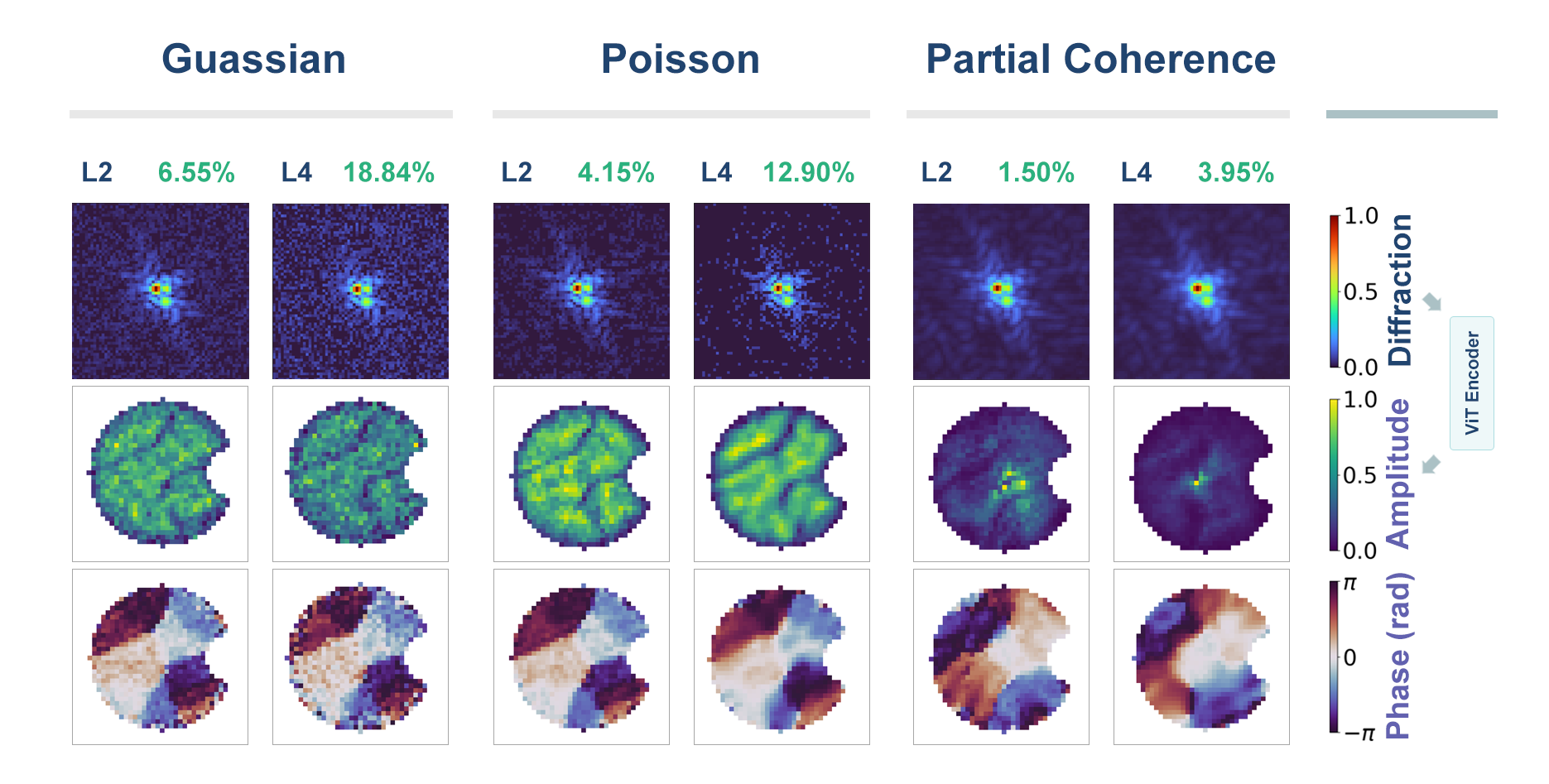
Экспериментальные данные, получаемые в ходе исследований, неизбежно подвержены воздействию шумов различной природы. Для оценки устойчивости разработанного алгоритма восстановления фазы мы моделируем два основных типа шумов: пуассоновский ( $P<a href="https://top-mob.com/chto-takoe-stabilizator-i-dlya-chego-on-nuzhen/">ois</a>sonNoise$ ) и гауссовский ( $GaussianNoise$ ). Пуассоновский шум возникает из-за дискретной природы фотонов и проявляется как случайные флуктуации в количестве зарегистрированных фотонов, особенно заметные при низких уровнях сигнала. Гауссовский шум, напротив, характеризуется нормальным распределением вероятностей и часто возникает из-за электронных помех в измерительном оборудовании и теплового шума. Включение этих типов шумов в процесс моделирования позволяет всесторонне оценить способность алгоритма эффективно подавлять артефакты и обеспечивать точное восстановление фазы даже в условиях зашумленных данных.

Для повышения точности реконструкции и снижения влияния шумов в процессе восстановления данных, применяются методы регуляризации полной вариации (Total Variation Regularization) и ограничения области поддержки (Support Constraint). Регуляризация полной вариации способствует сглаживанию решения, уменьшая шум, сохраняя при этом резкие границы объектов. Ограничение области поддержки, в свою очередь, задает априорные знания о расположении реконструируемого объекта, исключая решения, выходящие за пределы этой области, что особенно полезно при работе с данными, содержащими значительный уровень шума и артефактов. Комбинация этих методов позволяет получить более стабильные и достоверные результаты реконструкции, даже в условиях низкой SNR.

Процесс симуляции синтетических кристаллов включает в себя случайное размещение начальных точек, генерацию во́роновских областей с фазами в диапазоне <span class="katex-eq" data-katex-display="false">[-\pi,\pi]</span>, построение амплитудной маски кристалла и вычисление магнитуды дифракции с помощью быстрого преобразования Фурье (FFT), причем все изображения имеют размер <span class="katex-eq" data-katex-display="false">64\times 64</span> пикселей. — Процесс симуляции синтетических кристаллов включает в себя случайное размещение начальных точек, генерацию во́роновских областей с фазами в диапазоне $[-\pi,\pi]$ , построение амплитудной маски кристалла и вычисление магнитуды дифракции с помощью быстрого преобразования Фурье (FFT), причем все изображения имеют размер $64\times 64$ пикселей.

Результаты и Влияние на Материаловедение

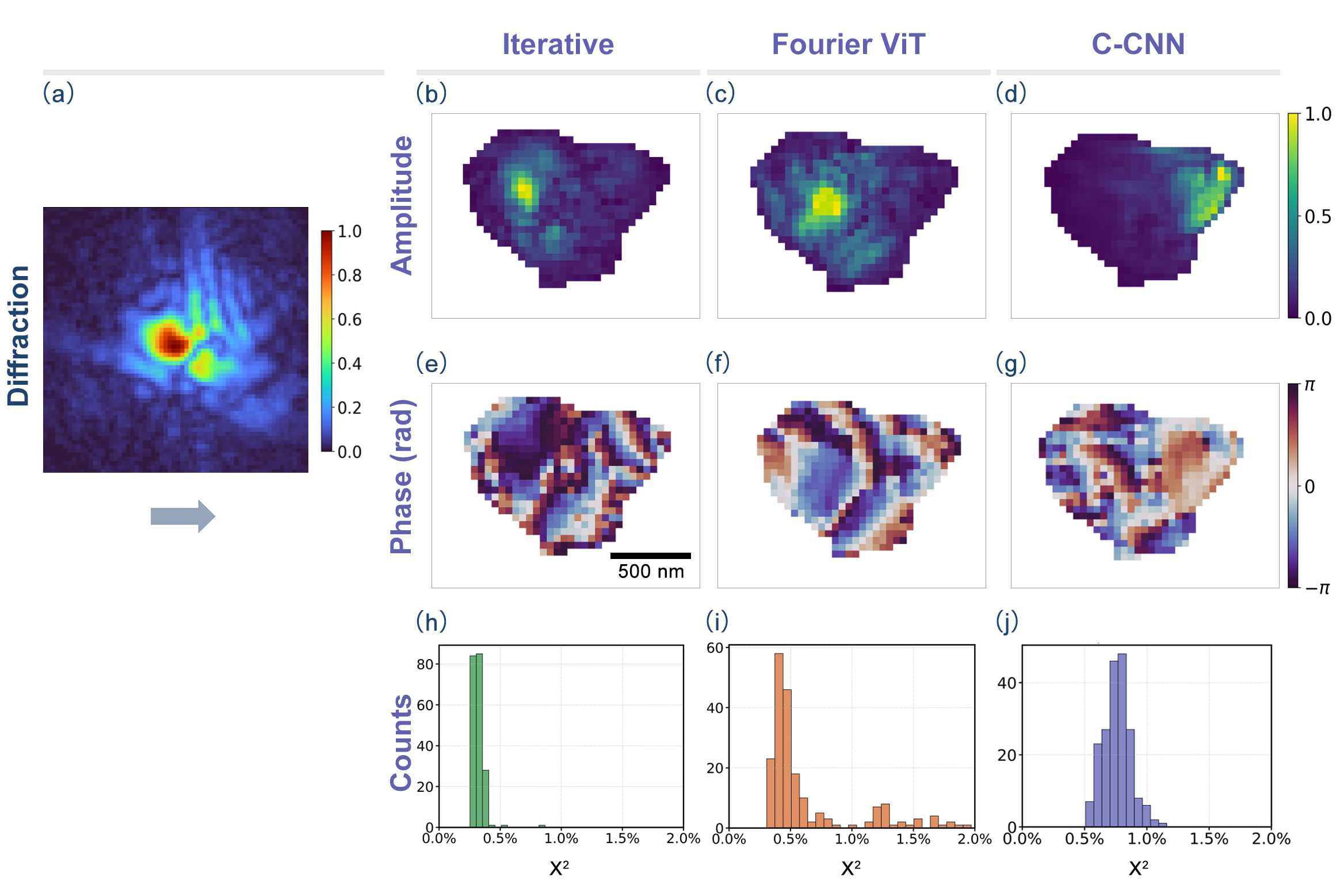
Количественный анализ с использованием метрики $MeanSquaredError$ продемонстрировал превосходство Vision Transformer над традиционными методами в задаче реконструкции сложных кристаллических структур. Данный подход, основанный на архитектуре трансформеров, изначально разработанной для обработки изображений, позволяет эффективно учитывать пространственные взаимосвязи между атомами в кристалле, обеспечивая более точное восстановление его трехмерной структуры. В ходе исследований установлено, что Vision Transformer не только превосходит существующие алгоритмы по точности, но и демонстрирует повышенную устойчивость к шумам и неполноте данных, что особенно важно при анализе реальных экспериментальных данных. Такое значительное улучшение в точности реконструкции открывает новые возможности для детального изучения и моделирования свойств материалов на атомном уровне.

Алгоритм продемонстрировал высокую устойчивость к шумам, сохраняя точность реконструкции даже в сложных экспериментальных условиях. Это особенно важно, поскольку реальные экспериментальные данные часто содержат значительные помехи, вызванные ограничениями оборудования или условиями проведения измерений. Исследования показали, что даже при увеличении уровня шума, метод продолжает надежно определять структуру кристалла, что позволяет получать достоверные результаты даже из неидеальных данных. Такая устойчивость к шумам значительно расширяет возможности применения алгоритма в материаловедении, позволяя анализировать материалы, полученные в различных, иногда неоптимальных, условиях и извлекать из этих данных ценную информацию о структуре и свойствах вещества.

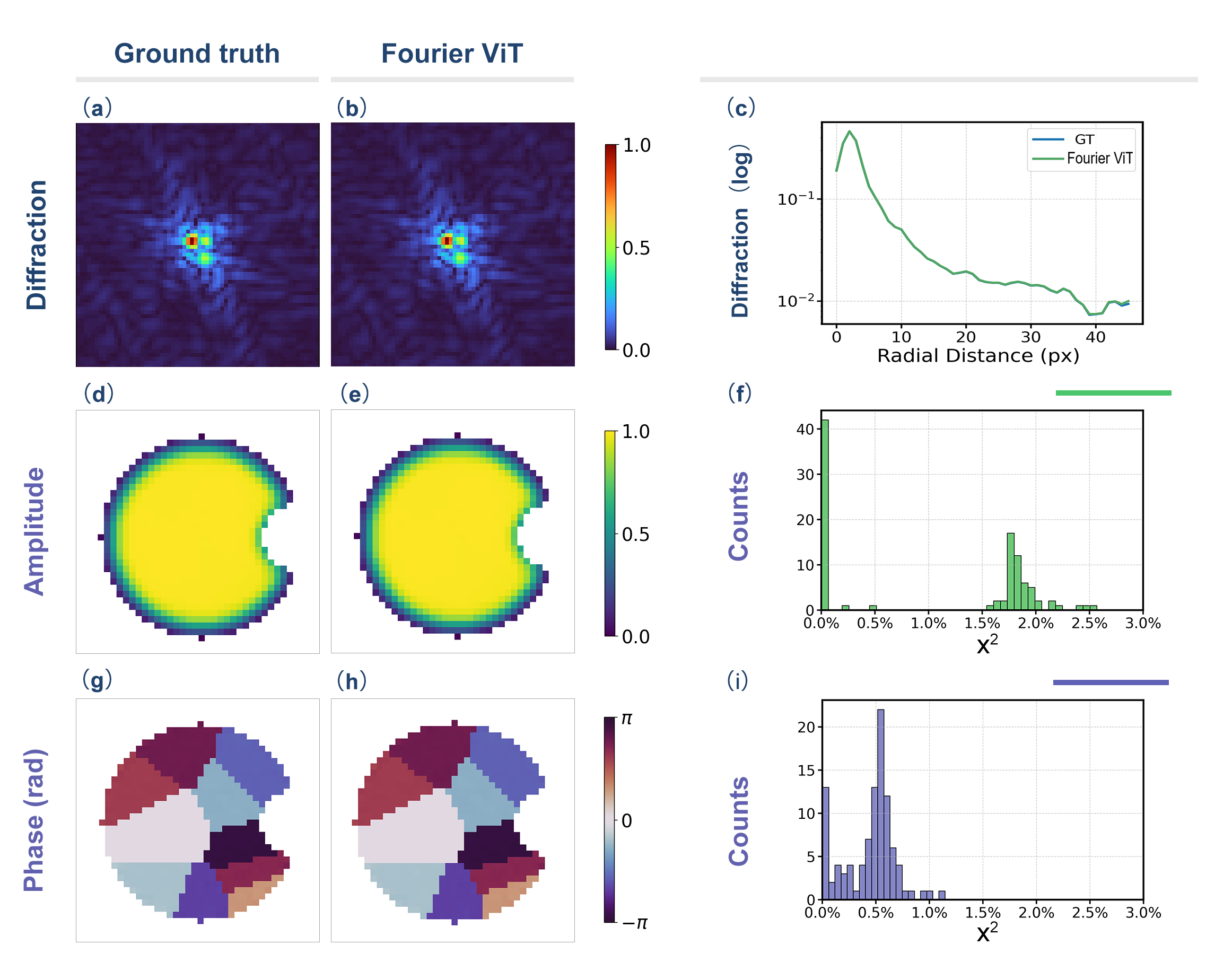
Достижение значения несовпадения в обратном пространстве (χ²) всего 0,35% при работе с синтетическими данными подтверждает высокую точность разработанного метода. Данный показатель, характеризующий степень соответствия между предсказанной и реальной кристаллической структурой, свидетельствует о способности алгоритма к детальному и корректному восстановлению сложных материалов. Низкое значение χ² указывает на минимальные погрешности в определении положения атомов и, следовательно, на надежность полученных результатов, что критически важно для дальнейшего анализа и моделирования свойств материалов.

Исследование продемонстрировало высокую точность предложенного метода при анализе реальных материалов. В частности, при работе с многодоменным кристаллом LCMO, удалось добиться значения расхождения в пространстве обратных решеток (χ²) всего 0.30%. Этот результат свидетельствует о способности алгоритма достоверно реконструировать сложные кристаллические структуры даже в условиях неоднородности и дефектов материала. Низкое значение χ² указывает на минимальное отклонение между предсказанной и фактической структурой, что открывает возможности для детального изучения и контроля над внутренним строением материалов и, как следствие, для разработки новых материалов с заданными свойствами.

Точное картирование внутренней структуры материалов, обеспечиваемое данной методикой, открывает возможности для выявления дефектов и полей напряжений, что является ключевым фактором для понимания их свойств. Выявление даже незначительных структурных отклонений позволяет оценить влияние этих дефектов на функциональные характеристики материала, такие как прочность, проводимость или магнитные свойства. В частности, анализ полей напряжений позволяет прогнозировать поведение материала под нагрузкой и оптимизировать его структуру для достижения заданных эксплуатационных характеристик. Полученные данные имеют решающее значение для разработки новых материалов с улучшенными свойствами и повышения надежности существующих.

Данное достижение открывает широкие перспективы в материаловедении, предоставляя возможность целенаправленного проектирования и оптимизации материалов с заданными функциональными характеристиками. Точное картирование внутренней структуры позволяет не только выявлять дефекты и поля напряжений, оказывающие существенное влияние на свойства материалов, но и предсказуемо модифицировать их состав и архитектуру для достижения желаемых параметров. Это особенно важно при создании новых поколений материалов для энергетики, электроники и биомедицины, где требуется высокая точность и контроль над структурой на микро- и наноуровнях. Возможность моделирования и оптимизации свойств материалов до их физического синтеза значительно ускоряет процесс разработки и снижает затраты, открывая путь к созданию инновационных материалов с беспрецедентными характеристиками.

Визуализация устойчивости к шуму для Fourier ViT на уровнях 2 и 4 демонстрирует, что модель эффективно восстанавливает амплитуду и фазу кристаллов (40x40 пикселей) даже при наличии гауссовского, пуассоновского шума или частичной когерентности, что подтверждается значениями <span class="katex-eq" data-katex-display="false">\chi^{2}_{n}</span> (в процентах), отражающими погрешность дифракции по отношению к эталонному изображению (64x64 пикселей). — Визуализация устойчивости к шуму для Fourier ViT на уровнях 2 и 4 демонстрирует, что модель эффективно восстанавливает амплитуду и фазу кристаллов (40×40 пикселей) даже при наличии гауссовского, пуассоновского шума или частичной когерентности, что подтверждается значениями $\chi^{2}_{n}$ (в процентах), отражающими погрешность дифракции по отношению к эталонному изображению (64×64 пикселей).

Исследование демонстрирует, что применение Vision Transformer для восстановления фазы в когерентной дифракционной визуализации кристаллов с множеством доменов позволяет преодолеть ограничения традиционных методов. Авторы предлагают систему, где внимание, подобно локальным правилам, выстраивается вокруг Фурье-спектра, обеспечивая адаптацию к сложным структурам. Это согласуется с идеей о том, что порядок не нуждается в архитекторе, а возникает из локальных взаимодействий. Как однажды заметил Вильгельм Рентген: «Я не могу представить, что эти лучи будут иметь какое-либо практическое применение». Несмотря на эту первоначальную недооценку, его открытие, подобно представленному здесь подходу, демонстрирует силу наблюдения и анализа в раскрытии скрытых структур и возможностей.

Куда же это всё ведёт?

Представленная работа, демонстрируя возможности Vision Transformer в реконструкции фазы в когерентной дифракционной визуализации, лишь подсвечивает глубинную проблему: стремление к глобальному контролю над сложными системами. Очевидно, что многодоменные кристаллы, представляющие собой самоорганизующиеся структуры, не нуждаются в «архитекторе» — порядок возникает из локальных взаимодействий. Попытки навязать решение «сверху», пусть и посредством изящных алгоритмов, неизбежно сталкиваются с внутренними противоречиями системы. Успех подхода, вероятно, заключается не в абсолютной точности реконструкции, а в способности извлекать полезную информацию из хаотичного паттерна дифракции.

Очевидным направлением дальнейших исследований представляется отказ от жёстких предположений о структуре кристалла. Более того, представляется интересным исследование возможности использования представленных алгоритмов не только для реконструкции, но и для предсказания формирования доменов, рассматривая процесс как эволюционную оптимизацию. В конечном счёте, задача состоит не в том, чтобы «решить» проблему сильной фазы, а в том, чтобы научиться «влиять» на неё, понимая, что полный контроль — иллюзия.

Остаётся открытым вопрос о масштабируемости подхода к кристаллам с ещё более сложной и непредсказуемой структурой. Вероятно, дальнейший прогресс потребует интеграции методов машинного обучения с более фундаментальными физическими моделями, позволяющими учитывать не только дифракционную картину, но и динамику формирования структуры кристалла. Вместо поиска «идеального» алгоритма, представляется перспективным создание адаптивной системы, способной обучаться и эволюционировать вместе с изучаемым объектом.

Оригинал статьи: https://arxiv.org/pdf/2602.12255.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-02-15 05:19