За гранью традиционных методов: Решение задач с подвижными границами с помощью нейросетей

Автор: Денис Аветисян

Новый подход, основанный на неглубоких сетях Kolmogorov-Arnold, позволяет эффективно моделировать фазовые переходы и динамику границ раздела сред без использования данных измерений.

Пока крипто-инвесторы ловят иксы и ликвидации, мы тут скучно изучаем отчетность и ждем дивиденды. Если тебе близка эта скука, добро пожаловать.

Купить акции "голубых фишек"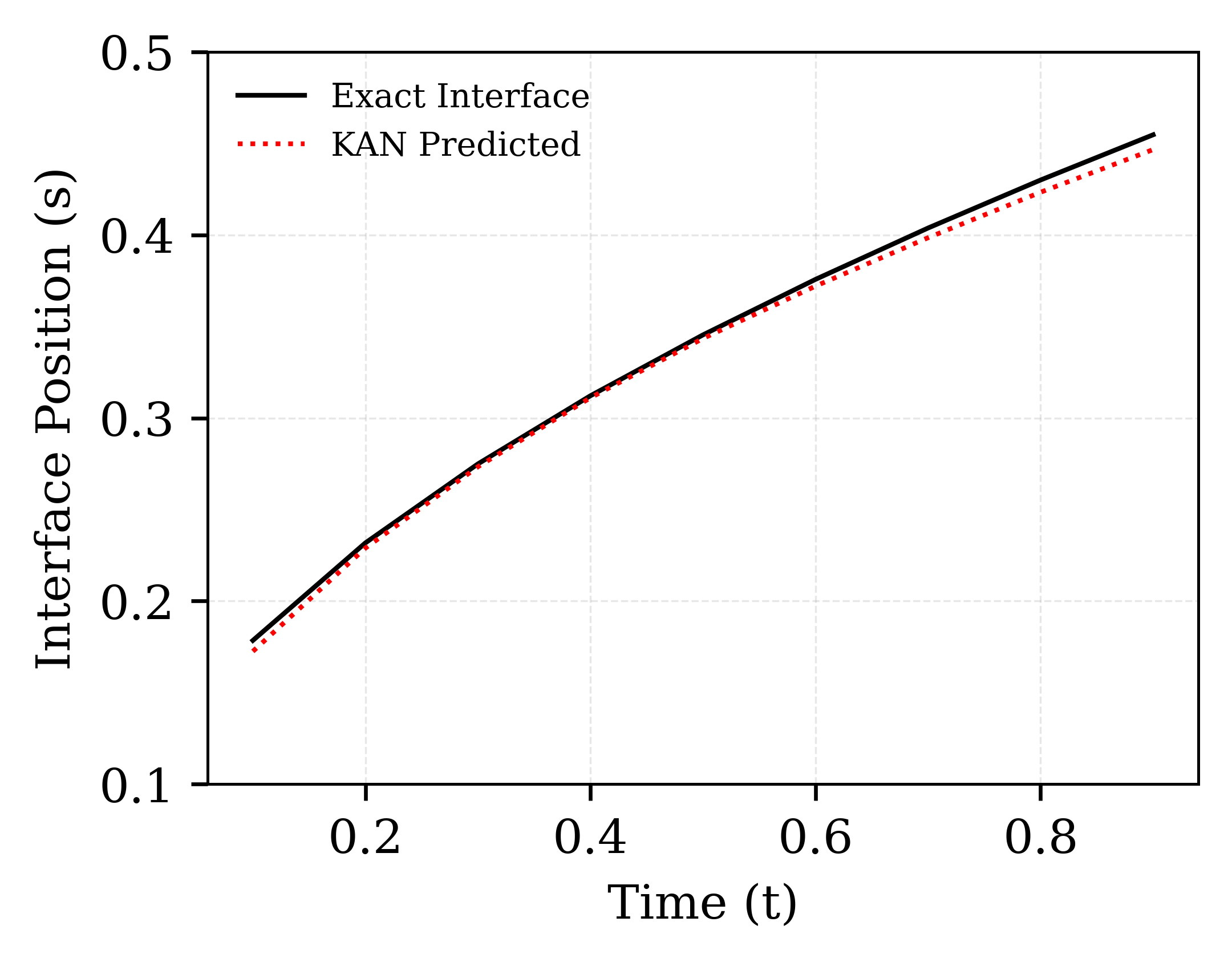

Температура и положение границы раздела фаз, рассчитанные методом KAN, демонстрируют высокую степень соответствия с точными решениями, что подтверждает надежность и точность предложенного численного подхода.

Представлен метод решения задач с подвижными границами, использующий неглубокие сети Kolmogorov-Arnold и превосходящий по эффективности традиционные методы, основанные на физически обоснованных нейронных сетях.

Решение задач с подвижными границами, таких как фазовые переходы, часто требует значительных вычислительных ресурсов и сложных численных схем. В данной работе, посвященной ‘Shallow-KAN Based Solution of Moving Boundary PDEs’, предложен новый подход, основанный на неглубоких сетях Колмагорова-Арнольда (KAN), для эффективного моделирования температурных полей и динамики интерфейсов. Показано, что предложенный метод, использующий физически обоснованные остатки и адаптивную передискретизацию, обеспечивает высокую точность и компактность по сравнению с традиционными нейронными сетями. Способны ли KAN-сети стать перспективной альтернативой для решения широкого класса задач с подвижными границами, не требуя при этом экспериментальных данных?

Вызов моделирования фазовых переходов

Моделирование фазовых переходов, таких как плавление и затвердевание, представляет собой сложную задачу из-за наличия подвижной границы между фазами. Эта граница, разделяющая, например, жидкое и твердое состояния вещества, постоянно изменяет свою форму и положение в процессе перехода, что требует от математических моделей и численных методов особого подхода. Традиционные методы часто испытывают трудности с точным отслеживанием этой динамичной границы, что приводит к погрешностям в прогнозировании поведения материала и требует значительных вычислительных ресурсов. Точное описание перемещения этой границы имеет решающее значение для оптимизации промышленных процессов в материаловедении и инженерии, включая литье, сварку и кристаллизацию.

Традиционные численные методы, применяемые для моделирования фазовых переходов, часто сталкиваются с серьезными трудностями при точном отслеживании движущейся границы раздела фаз. Эти методы, как правило, требуют чрезвычайно высокой вычислительной сетки вблизи этой границы для обеспечения приемлемой точности, что приводит к экспоненциальному росту затрат машинного времени и памяти. Проблема усугубляется необходимостью постоянной перестройки сетки для адаптации к изменяющейся форме интерфейса, что добавляет еще один уровень сложности и неэффективности. В результате, даже относительно простые процессы, такие как затвердевание металла или плавление льда, могут потребовать значительных вычислительных ресурсов и времени, ограничивая возможности детального анализа и оптимизации этих процессов в материаловедении и инженерии.

Точное прогнозирование поведения межфазной границы при фазовых переходах имеет решающее значение для оптимизации множества процессов в материаловедении и инженерии. От кристаллизации металлов и сплавов до процессов литья и сварки, понимание и контроль за движением этой границы позволяет значительно улучшить качество конечного продукта и эффективность производственных циклов. Например, в процессе литья, знание скорости затвердевания позволяет минимизировать дефекты и получить материалы с заданными свойствами. В материаловедении, моделирование фазовых переходов позволяет предсказывать формирование микроструктур и, следовательно, оптимизировать свойства материалов для конкретных применений. Таким образом, точное предсказание поведения межфазной границы — это не просто академическая задача, а ключевой фактор для развития передовых технологий и создания инновационных материалов.

Сравнение результатов, полученных с помощью KAN, с точным решением показывает соответствие как для распределения температуры, так и для положения границы раздела.

Физически обоснованные нейронные сети для задач Стефана

Сеть, обученная с использованием принципов физически-обоснованных нейронных сетей (PINN), решает задачу Стефана, интегрируя определяющие её физические законы непосредственно в функцию потерь. Вместо традиционного дискретизированного подхода, используемого в численных методах, PINN формулирует задачу как оптимизационную, где функция потерь включает в себя как ошибку соответствия данным, так и ошибку, связанную с несоблюдением дифференциального уравнения теплопроводности $\frac{\partial u}{\partial t} = \alpha \frac{\partial^2 u}{\partial x^2}$ и краевых условий Стефана. Минимизация этой комбинированной функции потерь заставляет нейронную сеть научиться решениям, удовлетворяющим как математической модели, так и граничным условиям, без необходимости явного построения сетки или применения стандартных численных схем.

В основе подхода заключается в формировании функции потерь нейронной сети, включающей в себя как уравнение теплопроводности $\frac{\partial u}{\partial t} = \alpha \frac{\partial^2 u}{\partial x^2}$ , так и граничные (Штефана) условия, описывающие фазовый переход. Это позволяет сети обучаться решению задачи, удовлетворяя физическим законам напрямую, без необходимости использования традиционных методов дискретизации на сетках. Вместо численного решения дифференциальных уравнений на дискретных точках, сеть аппроксимирует решение в непрерывном пространстве, минимизируя расхождение между предсказаниями сети и физическими уравнениями, заданными в функции потерь. Таким образом, процесс решения не зависит от размера и структуры сетки, характерных для конечных разностей или конечных элементов.

Предложенный подход демонстрирует сопоставимую точность с традиционными методами решения задачи Стефана, при этом используя значительно более эффективную архитектуру нейронной сети. В частности, количество обучаемых параметров составляет всего 640, что существенно меньше, чем в физически информированных многослойных персептронах (MLP), где это число достигает приблизительно 1.2 x 10⁵. Такое снижение числа параметров не только уменьшает вычислительную сложность, но и потенциально снижает риск переобучения модели, обеспечивая более обобщенное решение.

Повышение точности с помощью адаптивной колиокации

Концентрация коллокационных точек вблизи подвижной границы существенно повышает точность решений, полученных с помощью физически информированных нейронных сетей (PINN) для задач Стефана. Эффективность данного подхода обусловлена тем, что именно в области границы происходит наиболее резкое изменение решения, и высокая плотность коллокационных точек позволяет более адекватно аппроксимировать градиенты и кривизну поля, определяющие эволюцию границы. Применение равномерно распределенных коллокационных точек часто приводит к недостаточной точности вблизи границы и, следовательно, к неточным результатам моделирования. Таким образом, адаптивное распределение коллокационных точек с акцентом на область подвижной границы является ключевым фактором для достижения высокой точности и эффективности при решении задач Стефана с использованием PINN.

Адаптивные методы ресемплирования динамически изменяют распределение коллокационных точек, основываясь на текущем положении подвижного интерфейса. Это достигается путем увеличения плотности точек в областях, непосредственно прилегающих к интерфейсу, и уменьшения плотности в удаленных регионах. Такой подход позволяет поддерживать высокое разрешение решения именно в критических областях, где происходят наиболее значимые изменения, и эффективно использовать вычислительные ресурсы, избегая избыточной детализации в менее важных зонах. Эффективность метода заключается в автоматической адаптации к форме и движению интерфейса в процессе решения задачи.

Анализ результатов показал, что прирост точности решения при использовании более 8000 точек коллокации становится незначительным. Данный факт указывает на сходимость полученного решения относительно плотности точек коллокации. Это демонстрирует эффективность адаптивного подхода, позволяющего достичь высокой точности, избегая избыточного увеличения числа точек и, следовательно, снижая вычислительные затраты. Практически, увеличение числа точек коллокации сверх указанного порога не приводит к существенному улучшению результатов, что подтверждает оптимальность выбранной стратегии адаптивной дискретизации.

Интеграция метода уровня с нейронными сетями

Метод уровня представляет собой надежный и гибкий математический подход к отслеживанию и моделированию движущихся границ и сложных форм. В основе метода лежит идея представления границы как изоповерхности функции уровня, что позволяет автоматически адаптироваться к изменениям топологии границы, таким как слияние или разделение. Этот подход особенно полезен при моделировании задач, где геометрия движущейся границы существенно меняется со временем, например, при фазовых переходах, течении жидкостей или росте кристаллов. В отличие от других методов, требующих явного отслеживания точек на границе, метод уровня использует неявное представление, что обеспечивает повышенную устойчивость и точность, особенно в сложных геометриях и при больших деформациях. $\Phi(x,t) = 0$ определяет движущуюся границу, где Φ — функция уровня.

Сочетание метода уровня с нейронными сетями, обученными посредством физически информированного подхода (PINNs), и адаптивной колиокацией открывает новые возможности для точного и эффективного моделирования сложных фазовых переходов. Традиционно, численные методы, используемые для таких задач, сталкиваются с трудностями при отслеживании движущихся границ раздела фаз и требуют значительных вычислительных ресурсов. В данном подходе, метод уровня обеспечивает надежное представление геометрии границы, а PINNs, обученные на основе уравнений, описывающих физические процессы, позволяют решать эти уравнения без необходимости построения явной сетки. Адаптивная колиокация, динамически изменяя расположение точек, обеспечивает высокую точность даже в областях с высокой кривизной или сложными потоками. В результате, удается существенно снизить вычислительные затраты и повысить точность моделирования широкого спектра явлений, включая затвердевание сплавов, плавление материалов и другие процессы, где ключевую роль играет динамика фазовых границ.

Интеграция метода уровня с нейронными сетями открывает широкие возможности для управления материалами и процессами их обработки. В частности, становится возможным точный контроль над фазовыми переходами, что критически важно при создании новых сплавов и оптимизации процессов затвердевания. Эта комбинация методов позволяет моделировать сложные геометрические формы и динамику изменений с высокой точностью, что находит применение в различных областях инженерии, включая литье под давлением, 3D-печать и разработку композитных материалов. $\frac{d\phi}{dt} + \nabla \cdot (v \phi) = 0$ — данное уравнение описывает эволюцию функции уровня, и точное его решение, обеспечиваемое данной интеграцией, позволяет оптимизировать производственные процессы и создавать материалы с заданными свойствами.

Расширение возможностей для сложных геометрий и сценариев

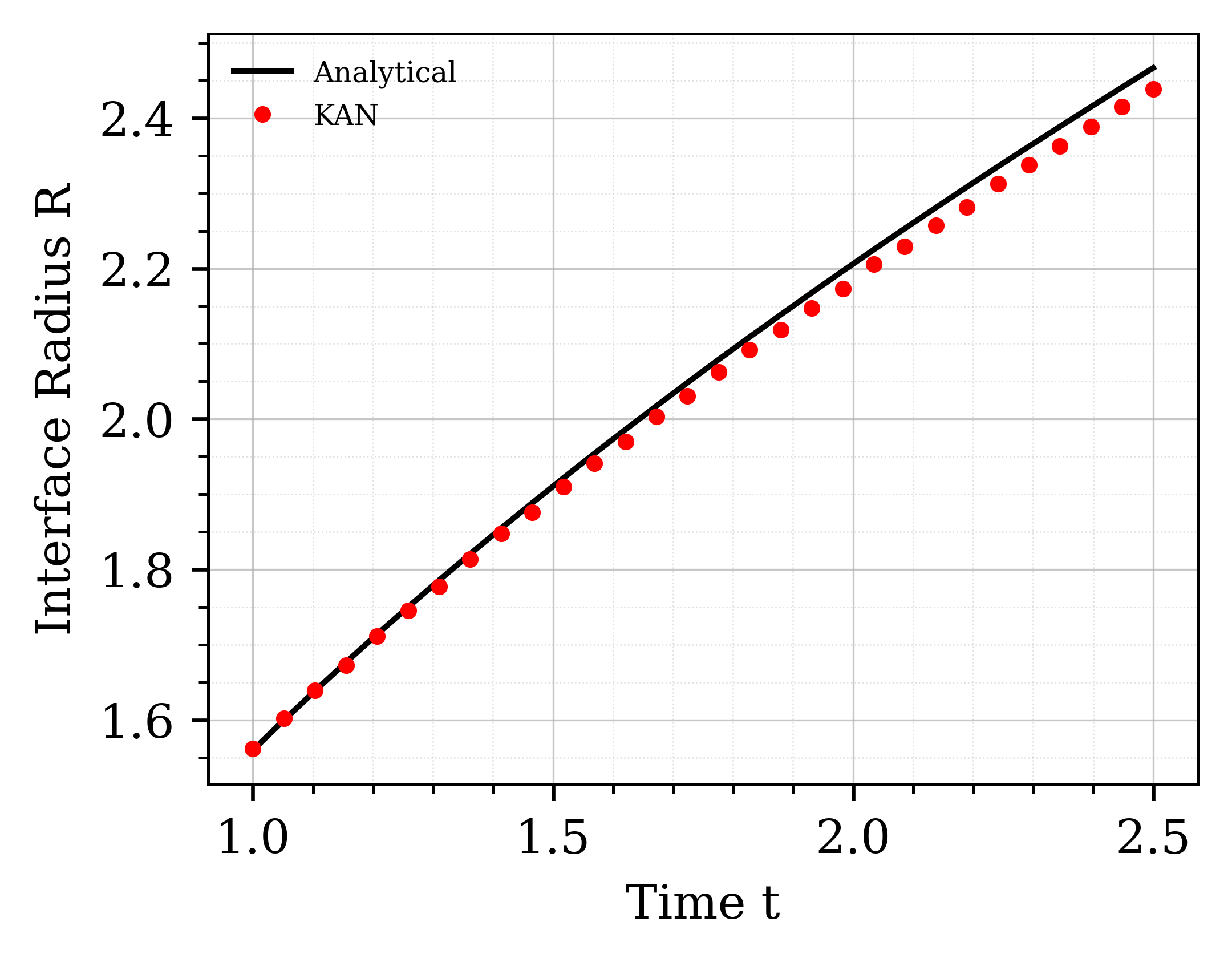
Предложенная методология демонстрирует высокую адаптивность и успешно применяется к решению более сложных задач типа Стефана, включая, в частности, проблему Франка с ее характерной круговой границей раздела фаз. В отличие от традиционных подходов, испытывающих трудности при обработке нетривиальной геометрии, данная методика позволяет точно моделировать динамику границы раздела даже в случаях сложной конфигурации. Это достигается за счет использования численных методов, адаптированных для эффективной обработки криволинейных границ, что открывает возможности для анализа и оптимизации процессов, где форма границы раздела играет ключевую роль, например, в кристаллизации, затвердевании сплавов и других материаловедческих задачах. Возможность корректного моделирования таких процессов позволяет значительно повысить точность прогнозирования и, как следствие, улучшить качество конечного продукта.

Точное отслеживание динамики границы раздела фаз в процессе изменения состояния вещества открывает возможности для оптимизации параметров технологических процессов. В частности, детальное понимание того, как граница раздела перемещается и эволюционирует, позволяет точно контролировать скорость затвердевания, охлаждения или плавления материала. Это, в свою очередь, способствует улучшению качества конечного продукта, снижению дефектов, таких как трещины или пористость, и повышению механических свойств. Например, в процессе литья металлов, точное моделирование движения границы раздела позволяет оптимизировать параметры охлаждения для получения отливок с требуемой микроструктурой и минимальными внутренними напряжениями. Таким образом, улучшенное понимание и контроль динамики границы раздела фаз является ключевым фактором для повышения эффективности и качества производства материалов.

Перспективные исследования направлены на интеграцию методов количественной оценки неопределенностей и систем управления в реальном времени, что позволит значительно расширить возможности разработанного подхода. Внедрение алгоритмов, учитывающих вариативность исходных данных и неточности измерений, обеспечит более надежные и устойчивые результаты моделирования процессов, описываемых задачей Стефана. Параллельно, разработка систем управления в реальном времени позволит адаптировать параметры технологических процессов непосредственно в ходе их реализации, оптимизируя качество продукции и минимизируя затраты. Такой симбиоз количественной оценки неопределенностей и оперативного управления открывает новые горизонты для применения данного подхода в различных областях материаловедения и инженерии, позволяя создавать более эффективные и предсказуемые технологические решения.

Представленная работа демонстрирует элегантность подхода к решению задач с подвижными границами, используя неглубокие сети Колмагорова-Арнольда. Подобно тому, как художник создает гармоничную композицию из ограниченного набора элементов, авторы эффективно используют архитектуру KAN для точного захвата динамики фазовых переходов. Именно красота масштабируется, а беспорядок нет — эта закономерность проявляется и здесь: вместо сложного наращивания параметров, достигается превосходная точность и эффективность. Как заметил Жан-Поль Сартр: «Существование предшествует сущности». В данном исследовании, решение проблемы предшествует определению сложной модели, что подтверждает изящество и функциональность предложенного подхода.

Куда же дальше?

Представленная работа, несомненно, демонстрирует элегантность подхода, позволяя обходить некоторые сложности, присущие традиционным методам решения задач с подвижными границами. Однако, подобно любому решению, оно не является абсолютным. Очевидным направлением для дальнейших исследований представляется расширение применимости данного фреймворка к задачам, включающим более сложные физические явления — например, многофазные течения или химические реакции на границе раздела фаз. Упрощение, пусть и изящное, всегда требует компромиссов, и необходимо тщательно оценить влияние этих компромиссов на точность и устойчивость решения в различных сценариях.

Особый интерес вызывает возможность интеграции представленного подхода с другими методами машинного обучения. Гибридные модели, сочетающие сильные стороны как физически информированных нейронных сетей, так и, скажем, генетических алгоритмов, могут позволить автоматизировать процесс выбора оптимальной архитектуры сети и параметров обучения, тем самым расширяя область применимости и повышая эффективность решения. Игнорировать потенциал для адаптации к данным, даже если они не используются напрямую в процессе обучения, было бы неразумно.

В конечном счете, истинное мерило ценности любого метода — это не его теоретическая красота, а его способность решать реальные, практически значимые задачи. Следующим шагом представляется не просто демонстрация работоспособности подхода на модельных примерах, а его применение к задачам, возникающим в инженерии, материаловедении или геофизике. Только тогда станет ясно, насколько глубоко данная архитектура способна уловить тонкости поведения сложных систем.

Оригинал статьи: https://arxiv.org/pdf/2601.09818.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-01-18 22:21